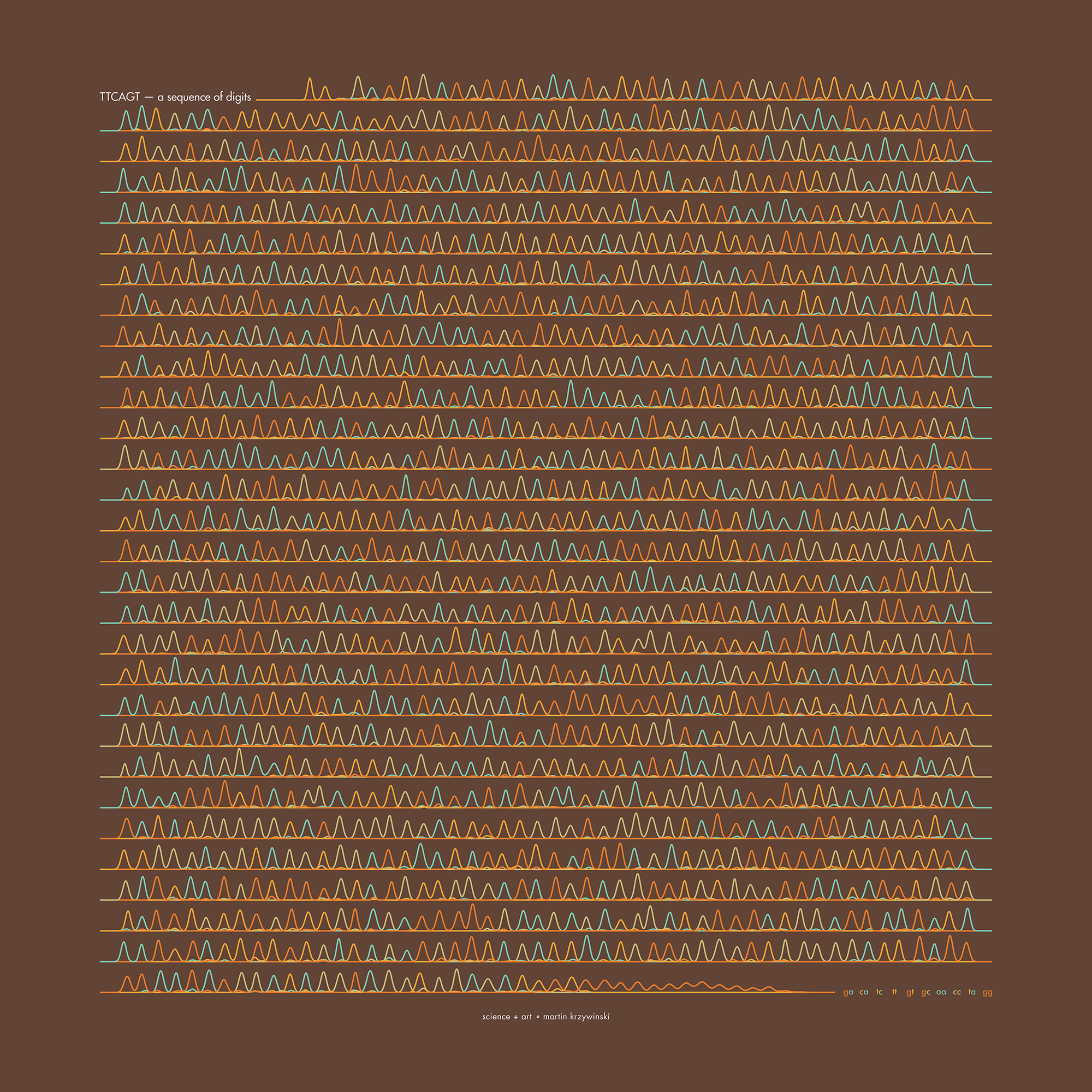 buy artwork
buy artwork
Pi Day 2022 — three one four: a number of notes — A musical journey into the digits of Pi
On March 14th celebrate `\pi` Day. Hug `\pi`—find a way to do it.
For those who favour `\tau=2\pi` will have to postpone celebrations until July 26th. That's what you get for thinking that `\pi` is wrong. I sympathize with this position and have `\tau` day art too!
If you're not into details, you may opt to party on July 22nd, which is `\pi` approximation day (`\pi` ≈ 22/7). It's 20% more accurate that the official `\pi` day!
Finally, if you believe that `\pi = 3`, you should read why `\pi` is not equal to 3.
3 There you go
1 Straight
4 Number me not
1 Scales
5 There is more of me
9 To forget than you can remember
—Emma Beauxis-Aussalet (314... piku)
Welcome to 2022 Pi Day: a celebration of `\pi` and mathematics (and music).
In this section, we get into the mathematical story of each track. We also provide detailed “Composer's Notes”, in which Greg gives insight into his approach to the composition and the musical inspiration and theory behind it.
Track 1 — 314...
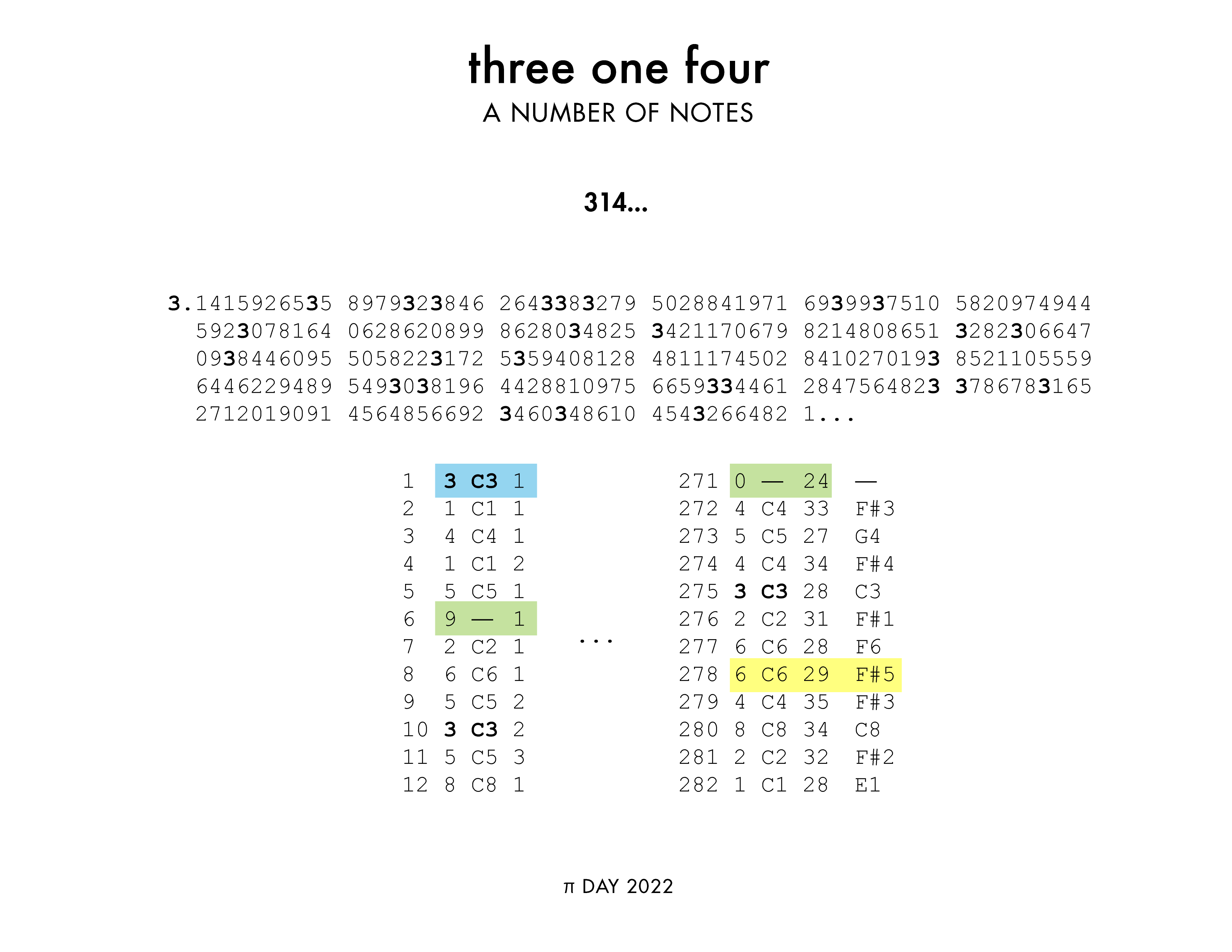
The track “314...” ( listen on Youtube ) plays the first 282 digits of Pi.
Each digit `n` is initially mapped onto a C at octave `n`. For example, 3 is mapped onto C3 (fig above, blue). Since C0 and C9 fall outside of the range of a piano, these digits are always interpreted as rests (green).
As we see the same digits again and again, its note is adjusted for volume and articulation (e.g. staccato). By the time we reach the end, the notes vary widely from their original C`n` assignment. For example, digit 278 is a 6. This is the 29th 6 in `\pi`, so the note is heavily serialized. It's pitch is as far as possible from C6 — it is now an F#, which is a tritone away from C.
To learn more, watch our discussion of the track .
composer's notes
“314...” adapts the concept of multiple serial techniques used by composers in the mid 20th Century like Pierre Boulez (1925–2016) and Karlheinz Stockhausen (1928–2007) but applies it in a more modern, less aggressive manner.
serialism
Serialism is a technique developed by Arnold Scoenberg (1874–1951) at the beginning of the 20th century. As a composer Schoenberg saw himself at a crossroads in music history — the possibilities of tonal music had been fully developed and explored over the previous 300 years by composers like Bach, Beethoven, Brahms, Mahler and Wagner, so how was Schoenberg to continue this lineage without repeating it. His response was to create a style of music that is sometimes described as "atonal" i.e without a tonal centre.
The basic principle of Serialism is to order the 12 pitches of the chromatic scale from 1–12 (called a tone row) and then to generate all the melodic and harmonic material based on this tone row and variations of it. Schoenberg applied serialism to pitches only — he allowed himself to chose rhythms, articulations and dynamics in a more traditional music fashion.
the next 50 years
Moving ahead 50 years, the next generation of European composers took Schoenberg's serial technique and applied it to other musical elements including rhythm, dynamics and articulation. The result is music that is fiercely intellectual, challenging to listen to and difficult to perform. Since the 1970's the fierce intellectualism of music has faded and allowed space for more listenable music. Our piece “314...” navigates the line between accessible and difficult.
the tonal center
“314...” begins by establishing a tonal centre (C) and then rapidly moves away from having any tonal centre, reflecting the move from the familiar numbers of `\pi` to the less familiar.

Dynamics, articulation and pitch are serialised based on the frequency of occurrence of the digits 0–9 as we move through `\pi`. Dynamics are serialised in groups of every 8 occurrences, while both pitch and articulation are serialized in groups of 5 occurrences. Each group corresponds to a semitone change in pitch both above and below C, until we reach 6 semitones (tritone) above and below C, at this point we are as far away from C as possible tonally and so the piece ends abruptly.

Track 2 — Feynman Point
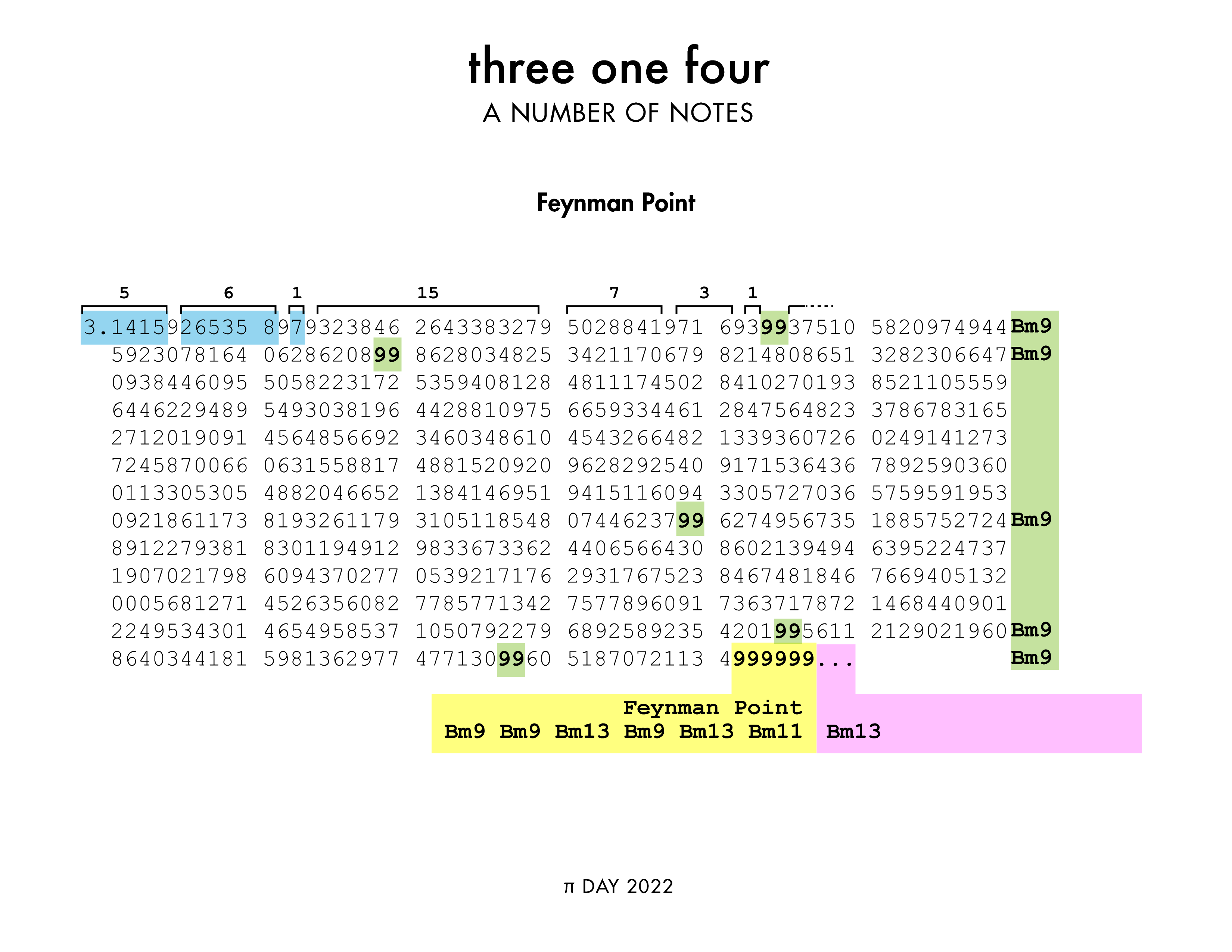
The track “Feynman Point” ( listen on Youtube ) tells Feynman's joke about the first time six 9's appear in `\pi`.
The Feynman point has appeared several times in my Pi Day art. Richard Feynman famously joked that it would be interesting to memorize `\pi` up to “where it goes 999999, so that I could recite it out loud, come to those six 9's, and then impishly say, "and so on!"”.
Our piece tells the joke as a sequence of B minor 9th chords. B because it's the "9th note of the alphabet" if we start at A and 9th chords because, well, duh! And why minor? Because we feel no joke should be too happy.
We mark off runs of digits in `\pi` between 9's (fig above, blue) and then use the number of digits in the sequence (5, 6, 1, 15, ...) to define the time signature. We develop rhythmic and jocular musical themes (the varying time signature makes sure that things don't line up to much). When we see a 99 we play a Bm9 as a left-right hand tremolo. Each time we see a 99 (there are five occurrences before the Feynman Point), we play a different inversion of Bm9.
When we get to the Feynman point, after accelerating to a dizzying pace (i.e., play as fast as you can), we play the chords Bm9, Bm9, Bm13, Bm9 and Bm11. Finally, to encode the "and so on..." we play a Bm13 arpeggio.
composer's notes
Feynman’s joke of reciting `\pi` until the first set of six 9’s is musically told with a playfully rhythmic texture, inspired by the musical logic and sense of humour of György Ligeti (1923-2006). Ligeti's piano music, particularly the two books of Etudes, stand as works of towering genius in the latter half of the 20th Century.
musica ricercata
The Feynman Point is more directly inspired by the Musica Ricercata — a collection of short piano works that each have an unerring sense of muscular musical development. This music is rhythmic and full of colour and tension — qualities that can be found in most of Ligeti's music.
the space between 9's
The piece begins with a pedaled B, which sets up a resonance in the piano chamber. Constantly changing time signatures are a feature of this piece which reflect the number of digits between successive 9’s.

riff and rhythm
The left hand plays a rhythmic octave figure in the bass, while the right hand plays a riff-like motif based on ascending octaves.

the feynman chord: Bm9
This material is broken up by vigorous B minor 9 chords, played as a tremolo between the two hands. These interruptions to the musical texture encode the five 99's that we see between the beginning of `\pi` and the Feynman Point.

punchline
The climax of the piece is at the Feynman Point, whose “999999” are performed as ascending B minor chords of varying extensions. The punchline of the joke — “and so on...” is a whimsical arpeggio.

Track 3 — Wallis Product
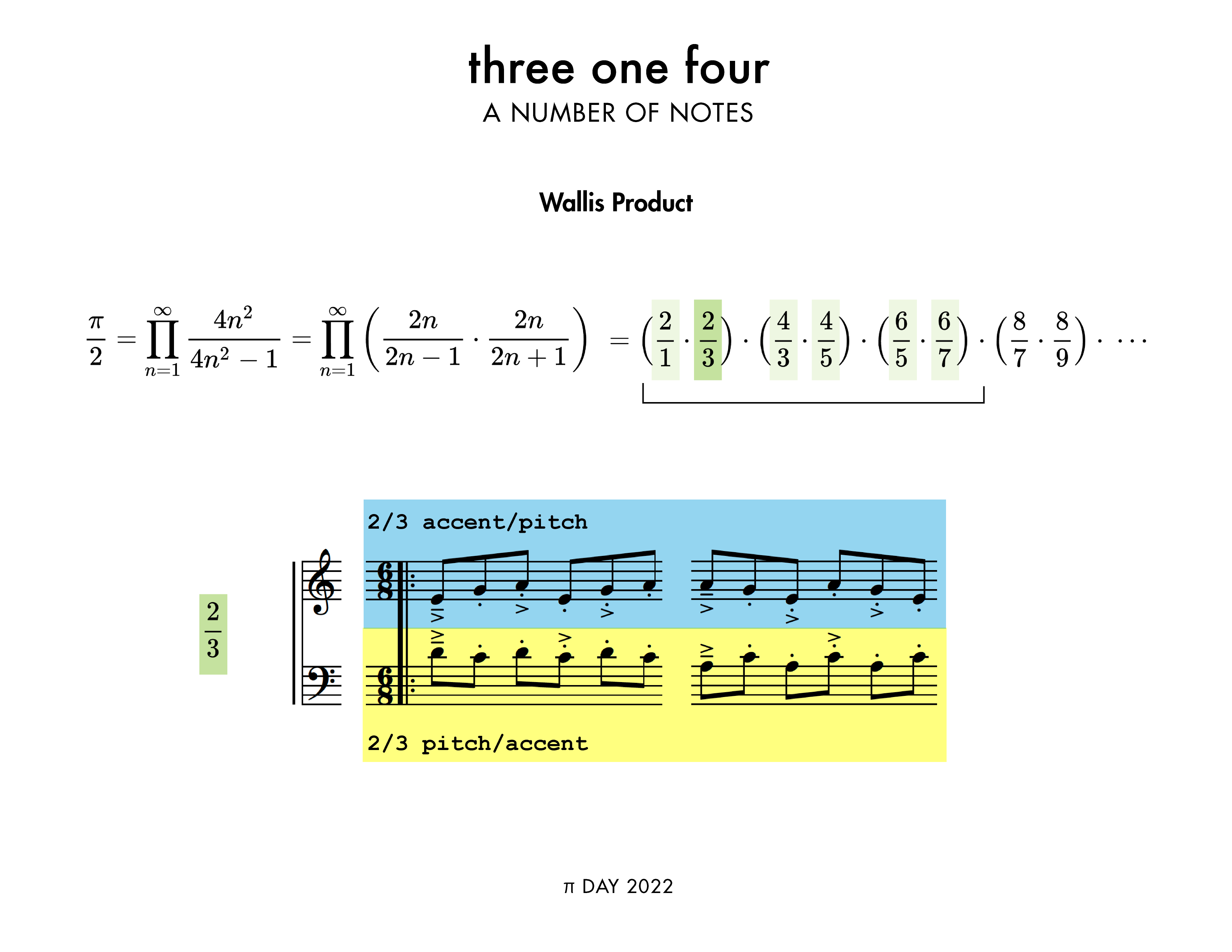
The track “Wallis Product” ( listen on Youtube ) represents the ratios in the Wallis Product as polyrhythms.
The Wallis Product is the only track that encodes an equation. In this case, the Wallis Product, which through a simple (but infinite) multiplication, gives you `\pi/4`.
The musical idea is very simple. For each of the six terms (fig above, green) in the product (e.g. `2/3`), the right hand plays a 2/3 accent/pitch polymeter (blue). This group of `2 \times 3 = 6` notes has 2 groups of 3 ascending pitches and 3 groups of accents. The left hand plays the descending melody and interprets the polyrhythms in an inverse way (yellow).
In this way, the pitch groupings of the right hand align with the accent groupings of the left, and vice versa.
We repeat the phrase four times to establish it and then again four times with reversed pitches.
composer's notes
The minimalist music of Steve Reich (1936–) and Phillip Glass (1937–) can be seen as an American response to the musical trends happening in post war Europe. Both Reich and Glass were influenced by the popular music of the time, as well as Jazz and traditional music from Africa. The music of both have penetrated deeply not only into musical culture, but into society at large — the Simpsons have referenced Reich's It's Gonna Rain)
rhythm and metre
The “Wallis Product” pays tribute to those giants of American minimal music. From early on it became apparent that the structure of the Wallis equation would be easily encoded into rhythm and metre, and this is how the piece was generated.
The music consists of layers of polyrhythms; each hand consists of a pitch group and a grouping outlined by accents. To allow the rhythmic nature of the piece to shine through, simple pentatonic melodies were chosen, and composed to fit under the fingers without too much movement.
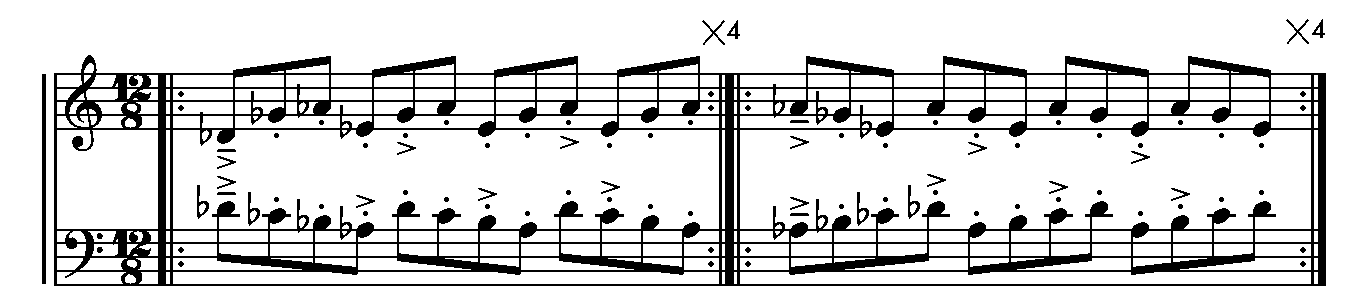
For example, in the excerpt above the right hand plays a group of three notes (D♭, G♭, A♭), but accents every four (a 4/3 accent/pitch polyrhythm). This pattern is then flipped in the left hand, where the pitch grouping is four, and the accent grouping is three. The accents line up with the pitch group of the opposite hand and the pitch groups line up with the accent groups of the opposite hand. The phrase takes `4 \times 3 = 12` notes to resolve and begins with a tenuto note to mark the start.
make it a duo
The “Wallis Product” is scored for a single performer but could easily be performed by two instrumentalists on almost any instrument.
listen in a different way
The combination of these polyrhythms creates a musical texture in which short, melodic motifs seem to pop out of the music. Minimal music, which on the surface can seem quite boring and repetitive, actually teaches people to listen in a different way. It demands that the listener direct their listening attention to one or two of the many different musical motifs that exist simultaneously, a kind of “choose your own adventure” and your own unique experience of the music.
Each time you listen to a piece of minimal music you can listen to a different aspect of the music. This interpretive role of the listener obviously exists for each musical experience, but it took minimal music to really make this experience explicit.
as the energy fades
One of the consequences of using the “Wallis Product” expression is that the terms increase in size as we progress through the sum, this results in the energy of the music falling away, as the distance between the rhythmic accents become greater. This decreasing of energy is counteracted by expanding the pitch range on the piano (we use higher and lower notes) before the piece abruptly comes to an end.

Track 4 — nn
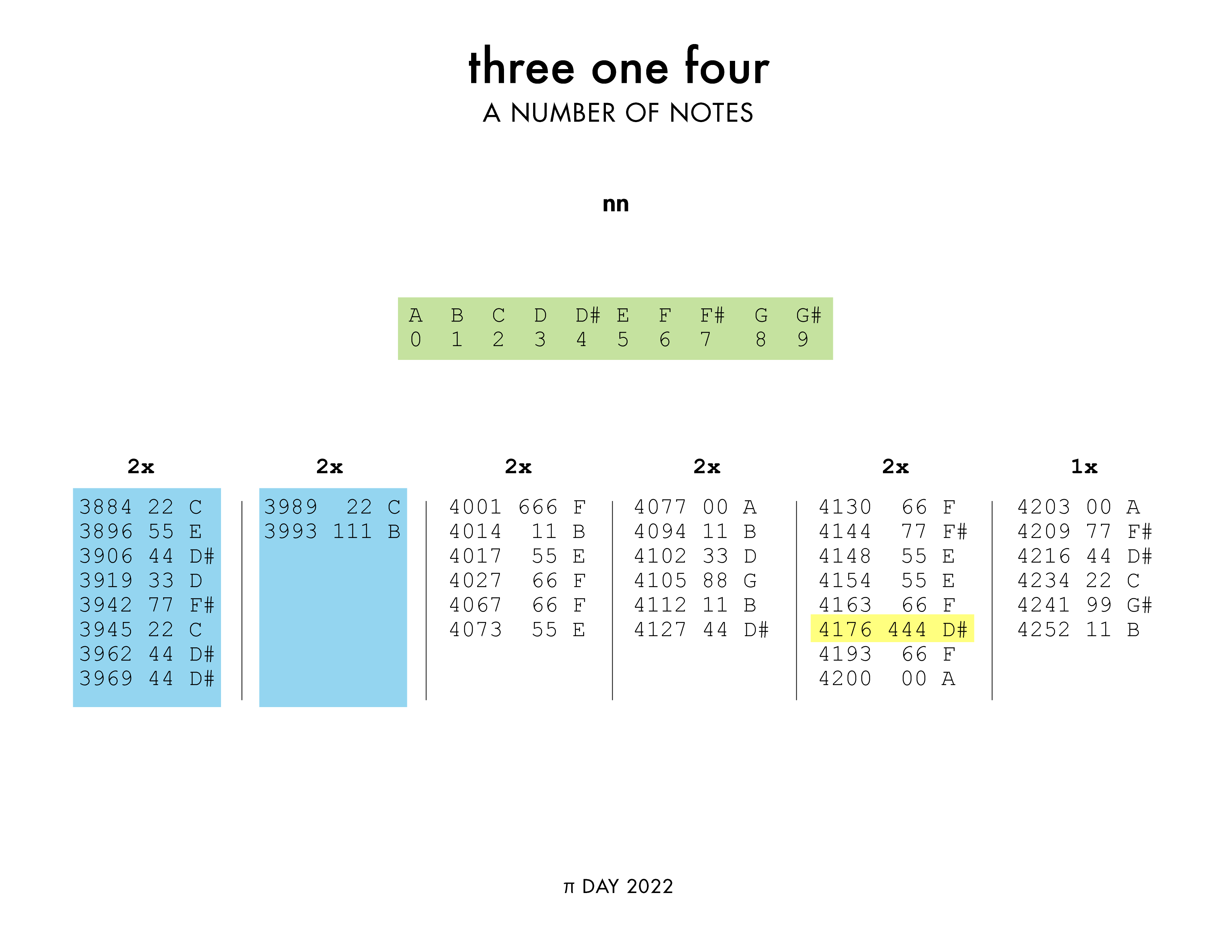
The track “nn” ( listen on Youtube ) helps you relax as you listen to digits pairing off.
For example, starting at digit index 3884, we come across the following pairs of repeated digits: 22 (3884), 55 (3896), 44 (3906), 33 (3919), 77 (3942), 22 (3945), 44 (3962), 44 (3969). These are mapped onto the musical phrase C E D# D F# C D# D#, with each note played twice and the final D# pair played an octave higher. A rest is introduced after the first D# pair to give the music a contemplative feeling. This phrase is repeated and followed by a phrase based on the next stretch of repeated digits.
The phrase lengths are 8, 2, 6, 6, 3, 5 and each of these is repeated. The final phrase is length 6 and is played once.
Satie was well known for leaving open-dended instructions to the performer. We have stayed faithful to this practise and provide directions that will make you think about pairing.
Solitaire? Alone? Disputez-vous prudemment Argue cautiously Demandez encore Ask again Sans réponse No answer Mais le compte est bon Yet it adds up On fait la paire malgré tout We pair up even so Argument circulaire Circular argument Aigre doux Bitter sweet Tombez sans plier Fall without folding
These directions were written by Emma Beauxis-Aussalet, who also wrote all the piku for the album.
The nn is not only relaxing but it is also the easiest to play. It is well within the reach of an advanced beginner, given a bit of practise.
composer's notes
Although not taken seriously as a composer by his contemporaries Claude Debussy (1862–1918) and Maurice Ravel (1875–1937), Erik Satie's (1866–1925) singular artistic voice has rung out from the beginning of the 20th century to the end. His music is generally simple and uncomplicated, but contained within it is an idiosyncratic element that immediately identifies his music to the listener.
Satie was as much an artist of ideas as music — when Debussy criticised his work as being without form, his next composition was titled Music In The Form of a Pear. You can almost hear him saying “It's not formless if it's in the shape of a pear!”. His furniture music (circa 1917) which was designed to fill space and not draw attention to itself predated muzak (circa 1935–1950) by several decades.
His piece Vexations is to be repeated 840 times, performances can last up to 35 hours.
His most well loved piano works, the Gymnopedies and Gnossiennes, were the inspiration for this work, in particular Gnossienne No. 3, which is characterised by repeated notes in the melody.

We chose a section of `\pi` where there was a suitable series of double digits, mapped those digits onto a scale (A, B, C, D, D#, E, F, F#, G, G#) and then composed a left hand accompaniment pattern similar in style to the Gnossienne.
Track 5 — null
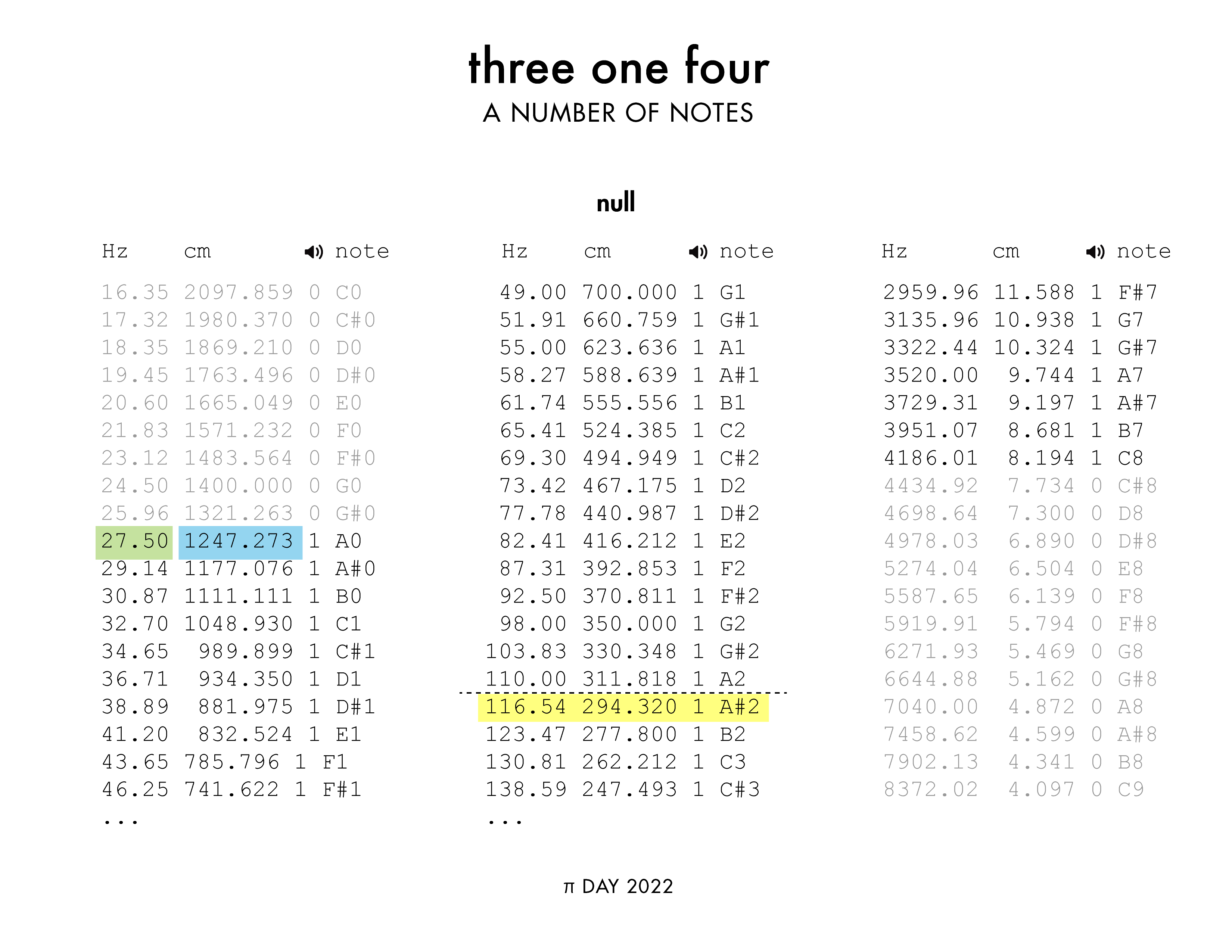
The track “null” ( listen on Youtube ) allows you to listen to the digits of `\pi` interpreted as sound wavelengths, forming various harmonics (some pretty and some not).
In the 12-step equal temperament tuning the frequency ratio between adjacent semitones is `\sqrt[12]{2}`. This way, when we advance 12 steps, we double the frequency.
The reference point is A4 = 440 Hz with the next two notes being A#4 = `440 \sqrt[12]{2} = 466.16 \textrm{ Hz}` and B4 `= 440 \sqrt[12]{2} \sqrt[12]{2} = 493.88 \textrm{ Hz}` and so on. The wavelength λ of each note is computed using `s`/`f` where `f` is the note frequency in Hz and `s` is the speed of sound in cm (34,300 cm/s). Thus, A4 has a wavelength of 77.95 cm. The lowest playable note on the piano is A0 (`\lambda = 1,247.273` cm) and the highest playable note is C8 (`\lambda = 8.194` cm).
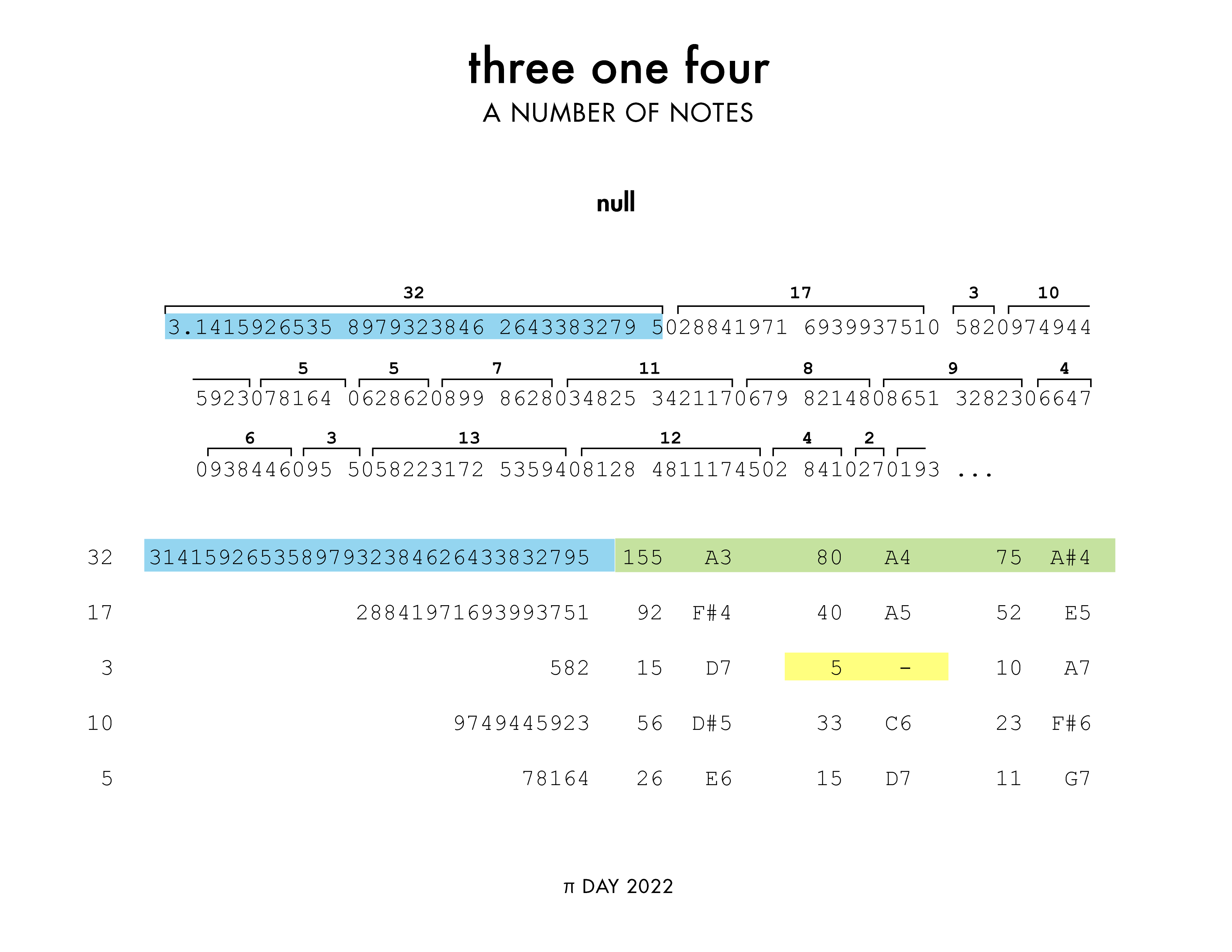
To convert digits to notes, the zeros in the digits of `\pi` are used to split digits into sequences. The sum of all the digits of the sequence `S` is calculated as are the partial sums of the first half of the digits `S_1` and second half `S_2`. For example, the first sequence is the 32-digit sequence
31415926535897932384626433832795
(the first zero in `\pi` is at digit 33). For this sequence, the sum is `S = 155` and the partial sums are `S_1 = 80` and `S_2 = 75`.
These sums are then interpreted as a wavelength of a note in units of centimeters and assigned the note closest in wavelength to the sum. For this process, the 12-step equal temperament tuning is used, as described above. The sums `S =155`, `S_1=80` and `S_2=75` are notes with the closest wavelengths are A3 (`\lambda = 155.909` cm) A4 (`\lambda = 77.95` cm) and A#4 (`\lambda =` 73.58 cm).
The left hand plays the lowest note, which is the one that corresponds to the largest of the three sums (`S`) and thus has the lowest pitch (e.g. A3). The right hand plays the two higher notes, which correspond to sums `S_1` and `S_2` (e.g. A4 and A#4).
Notes outside of the register (above C8) are encoded by rests.
The highest note played is thus C8. The lowest note corresponds to the sum `S = 294` of the longest sequence of digits (60 digits 1057–1116) and is an A#2 (yellow) with partial sums `S_1 = 162` (G#3) and `S_2 = 132` (C4).
Depending on the values of `S`, `S_1`, and `S_2`, the chord may have zero notes and be played as a rest (none of the notes are playable), one note (only lowest note is playable but `S_1` and `S_2` correspond to notes out-of-register), two notes (one of `S_1` or `S_2` is out-of-register) or three notes (all notes are playable). The unplayable scenarios arise when the digit sequence is short and the sums are small.
composer's notes
Morton Feldman (1926–1987) expressed a wish to never compose a piece of music that was louder than piano (quiet) and with this piece we pay tribute to Feldman’s unique and pioneering voice.
Feldman was an American contemporary to Pierre Boulez (1925–2016) and Karlheinz Stockhausen (1928–2007), but with a very different approach to composing music. Feldman's music is quiet and introspective, driven more by an aesthetic, intuitive response to sound, than by a desire for rigorous construction. His music seems suspended, full of tension — and yet not.
Our piece “null” is the searching for the void, the music with silence and space. The chords here are not linear narrative, but exist in their own space and for their own sake much like Feldman's. Given how we've selected the notes, some of our chords are quite pleasant — accidentally so. In Feldman's work, we often see an absence of such combinations.

Let the sounds wash over you and experience them directly without wanting them to “go anywhere” or “do anything”.
For me, this is the piece that comes the closest to representing the concept of `\pi` in musical language.
Track 6 — ...264

The track “...264” ( listen on Youtube ) is as far as we can go. It plays the last digits of `\pi`.
The world record `\\pi` computation (as of February 2022) was 62,831,853,071,750 digits by the Centre for Data Analytics, Visualisation and Simulation (DAViS) team at the University of Applied Sciences of the Grisons. The computation took 9,363,885.591 wall-clock seconds, generating, on average, 6,710,019.304 digits per second.

We encode the digits 0–9 are mapped onto notes using two interleaved pentatonic scales: the C penatonic scale (C D E G A) and the E♭ pentatonic scale (E♭ G♭ A♭ B♭ D♭), which are combined to create the decatonic scale C D♭ D E♭ E G♭ G A♭ A B♭ (green).
The piece depicts the last 119.591 seconds of the computation and plays notes sampled from the 802,457,882 digits that were calculated during this time (`119.591 * 6710019`). In each second of the music (blue), the right hand plays six notes sampled from a second of computation: first, second, mode (played twice), penultimate and last notes computed during that second.
The last bar of the track corresponds to the final 0.591 seconds, in which we play 3 notes that correspond to the last 3 known digits of `\pi` which are 264 (yellow).
The left hand harmonizes the sequence of digits with a jagged, jazz-inspired harmonies.
This track takes us to the end of the album. And the end of `\pi`.
For now.
Update on Jun 2022: The 62.8 trillion digit record was broken on March 2022 (after this album was mastered) by Emma Haruka Iwao who calculated 100 trillion digits. The last six digits of this calculation are ...295560. The contents of this track need to be updated as well as the title — to ...560.
composer's notes
The story of 20th century classical music is a tale of two continents — America and Europe. Each had their own cultural and historical precedents that shaped the music that composers were writing at this time.
Jazz was one of the influences on American composers of the latter half of the 20th century, particularly the minimalists like Steve Reich (1936–) and Phillip Glass (1937–) and John Adams (1947–).
the bebop era
When listening to the stream of notes that were the basis for this track (generated from roughly the “last” billion digits of `\pi`), my thoughts were of the solos of jazz pianists from the bebop era of the 40's and 50's, and moving into the free jazz era of the 70's. The relentless energy of these notes suggested to me the energy of American Jazz.
rhythm and dissonance
I took my cue from this style of music and generated a left hand accompaniment pattern that supports the right hand stream of notes. The left hand of jazz pianists were used as interjections to the right hand melodies — often they were very short and rhythmic and contained within them strong dissonant intervals.

“...264” utilizes this technique throughout the piece. At the beginning of the piece the left hand chords are sparse, but as the piece progresses they become interspersed with short melodic phrases. As the piece progresses the left hand material becomes increasingly melodic, so that we start to hear a more complex musical texture build.

The harmony modulates every ten bars based on a decatonic scale (C D♭ D E♭ E G♭ G A♭ A B♭). Starting on C, each chord change moves up a third (to C E♭m G B♭m D♭ Em A♭ Dm G♭ B♭m).
the final bars
In the final bars of the piece the harmony becomes much more dense as we hear the decatonic scale as chords, and melodies.

Beyond Belief Campaign BRCA Art
Fuelled by philanthropy, findings into the workings of BRCA1 and BRCA2 genes have led to groundbreaking research and lifesaving innovations to care for families facing cancer.
This set of 100 one-of-a-kind prints explore the structure of these genes. Each artwork is unique — if you put them all together, you get the full sequence of the BRCA1 and BRCA2 proteins.
Propensity score weighting
The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)
This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.
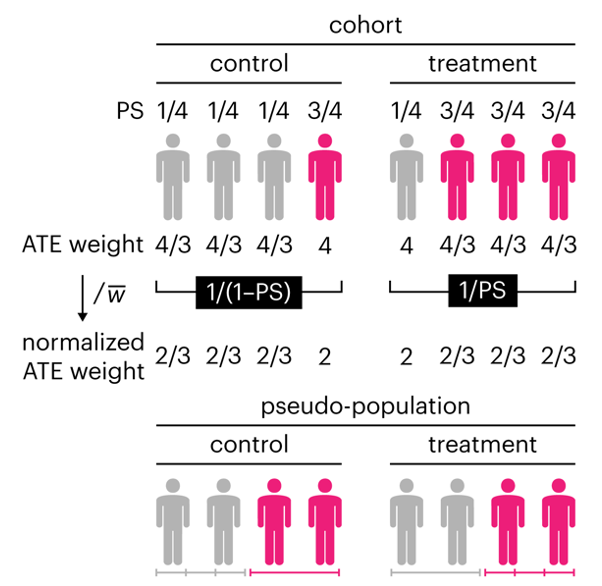
Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.
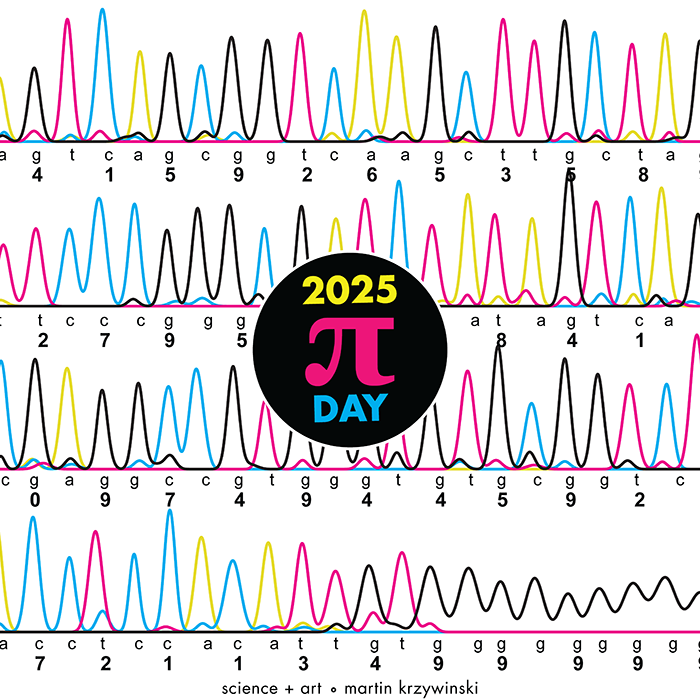
Happy 2025 π Day—
TTCAGT: a sequence of digits
Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.
Crafting 10 Years of Statistics Explanations: Points of Significance
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.
Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.
In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
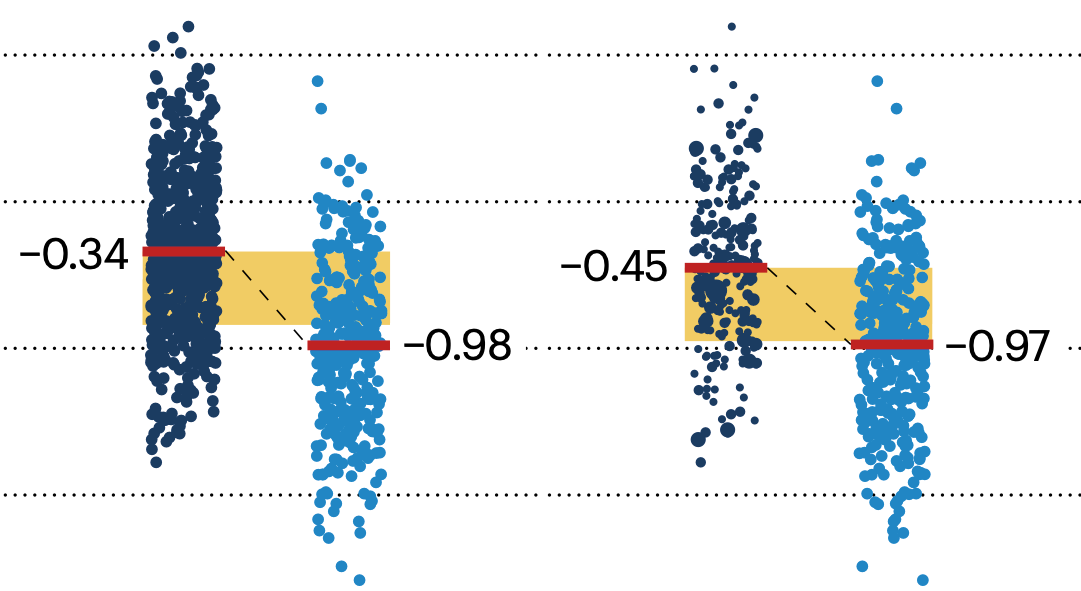
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Understanding p-values and significance
P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.
We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.
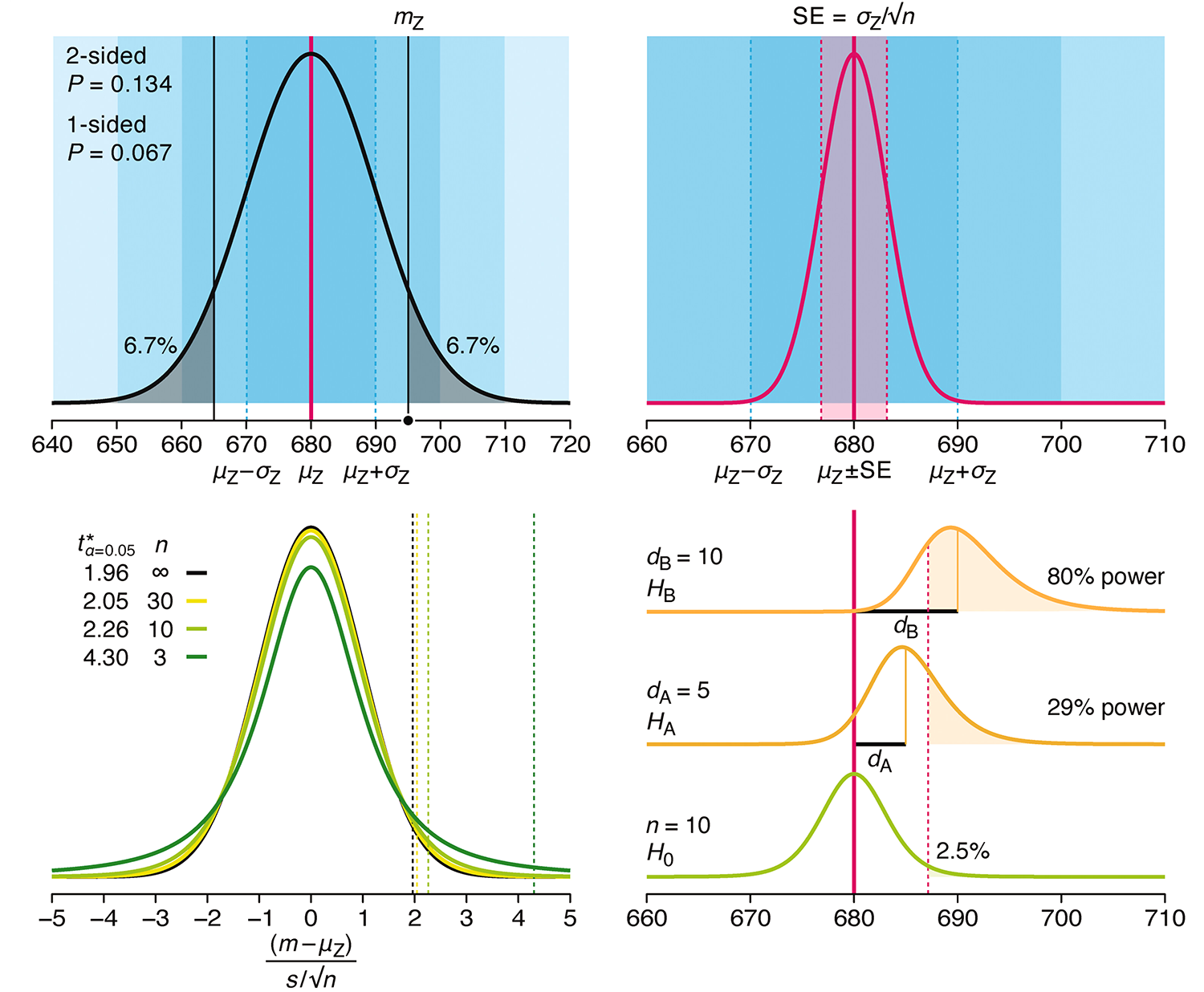
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.