The Ptolemaic Clock — A Proposal
contents
Consider the lowly wall clock. It's practical and generally tells the correct time. It's the same clock everywhere and after a while it gets boring pretty quickly—maybe now?

In the regular clock the face bezels stay in place and the hands move. Why am I telling you this? Well, maybe you see where I'm going.
Who says it's the hands that have to rotate? Instead of rotating hands and a stationary bezel, consider the clock with stationary hands rotating bezels.

In the Ptolemaic clock there are two independent bezels and two independent hands. The bezels rotate counterclockwise to simulate the standard clockwise motion of the hands. The hands are not moving but in the frame of reference of the bezels, it's the hands that are rotating. The position of the bezel is always related to the current time and the position of its corresponding hand.
The bezel can move clockwise.
Thanks to Rodrigo Goya for suggesting the name for this kind of clock—Ptolemaic Clock, named so after the geocentric Ptolemaic model of the solar system.
To tell the time on the Ptolemaic clock is a process identical to using the standard clock. You look at the bezel numbers at the ends of the hour and minute hands.
On the fixed bezel layout, most people will take a short cut and tell the time by the position of the hands. This works as long as you have a standard clock. On a Ptolemaic clock the position of the hands tells you nothing.
Here is a Ptolemaic clock telling us it is 6:30. It uses the same position of hands as in the figures above.
You know this because the blue hour hand points to midway between 6 and 7 on the inner hour bezel and the grey minute hand points to 30 on the outer minute bezel.

After 15 minutes, it's 6:45 and our Ptolemaic clock bezels have moved a little bit.

Can you tell what time it is on the Ptolemaic clock below?

Customizing your Ptolemaic clock is easy. Simply adjust the hands to desired positions and set the time by moving the bezels. The clock below shows the same time as the clock in the above figure — both show 8:50.

In the clock design shown here, the hands are the same size and only differ by color. To make things less confusing, emphasize the hour hand.
To make things more confusing, remove all color and number cues, keeping only a single symbol on each of the bezels to indicate 12 o'clock and 0 minutes. This is shown in the clock below.

Spice it up with multiple Ptolemaic clocks side-by-side telling the same time with different hand positions.
Suppose it is 2:30 in Vancouver—this is my location. The clocks below all show 2:30, but with hands set to 5:30, 11:30 and 7:30.

These hand positions are those that would appear on a standard clock showing the times in New York (5:30), Paris (11:30) and Tokyo (7:30).
Let's now use the Ptolemaic clock to show times at these three locations but with the hand set to the curiously satisfying layout of 10ish minutes to 2.

Set both hand positions to 12 o'clock and then remove the hands; to tell time, read the numbers on the hour and minute bezels at the apex of the clock.
Sophisticated implementations of the Ptolemaic clock could periodically randomize hand positions to keep things interesting; by the time you've figured out the time in the morning, you're wide awake.
Every minute the clock randomly resets its hand positions. The movement is smooth and the bezels follow.
If you would like to implement the Ptolemaic clock, I would be happy to hear from you. One should be able to take a regular wall clock, reverse the direction of the hand mechanism and rig a freely moving bezel to each of the minute and hour mechanism. The hands should not move and can be fixed to the front glass plate, for example.
Someone made templates for 3D printing a Ptolemaic clock.
It should now be clear that the Ptolemaic clock is superior to the standard clock. The reasons are
- it's much harder to tell time on the Ptolemaic clock, which makes your brain do more work
- it tips its hat off to a simpler time when we didn't know anything and hints at the possibility of regression anytime
- it will confuse everyone
- you have a great excuse for being late
- return to geocentric values!
- you can customize your own Ptolemaic clock by moving the hands to arbitrary locations
- two Ptolemaic clocks can have their hands and bezels at different positions but still be telling the same time
- two Ptolemaic clocks can have their hands at the same position but be telling different times
Beyond Belief Campaign BRCA Art
Fuelled by philanthropy, findings into the workings of BRCA1 and BRCA2 genes have led to groundbreaking research and lifesaving innovations to care for families facing cancer.
This set of 100 one-of-a-kind prints explore the structure of these genes. Each artwork is unique — if you put them all together, you get the full sequence of the BRCA1 and BRCA2 proteins.
Propensity score weighting
The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)
This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.
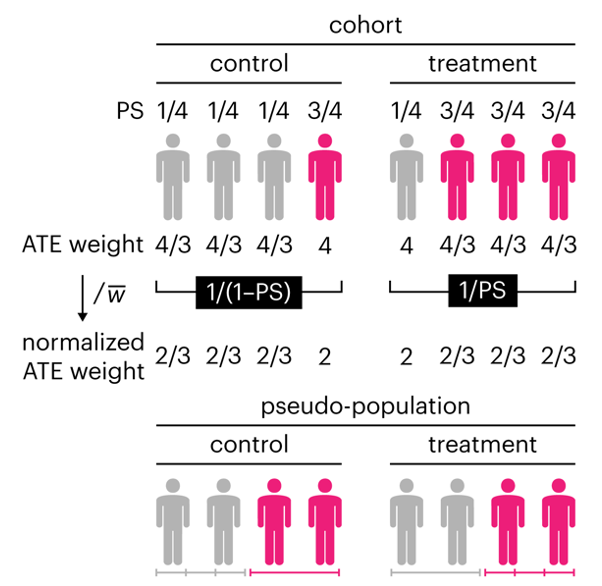
Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.
Happy 2025 π Day—
TTCAGT: a sequence of digits
Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.
Crafting 10 Years of Statistics Explanations: Points of Significance
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.
Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.
In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
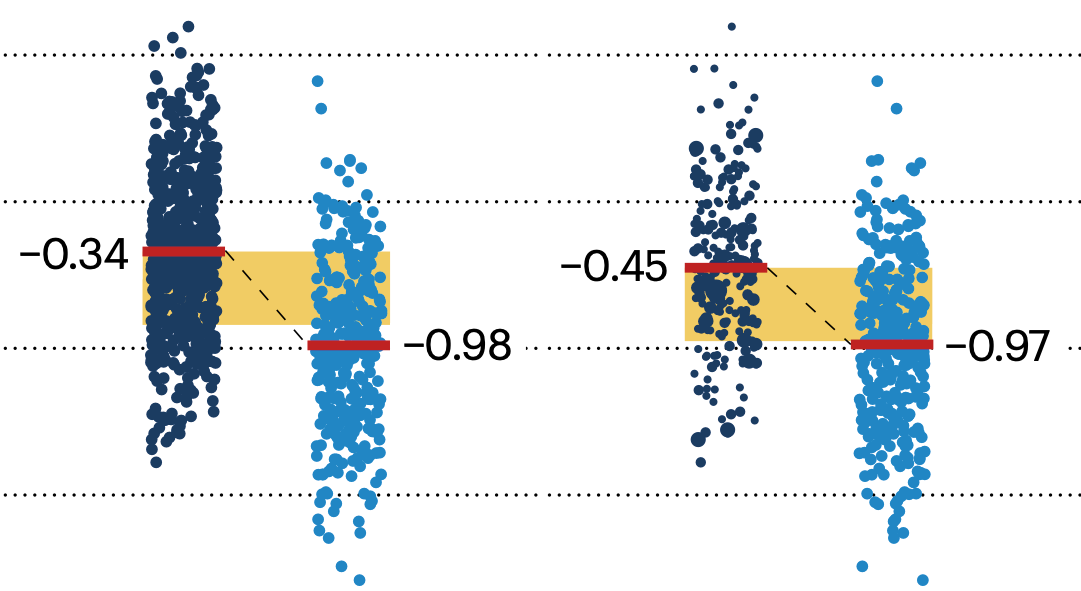
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Understanding p-values and significance
P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.
We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.
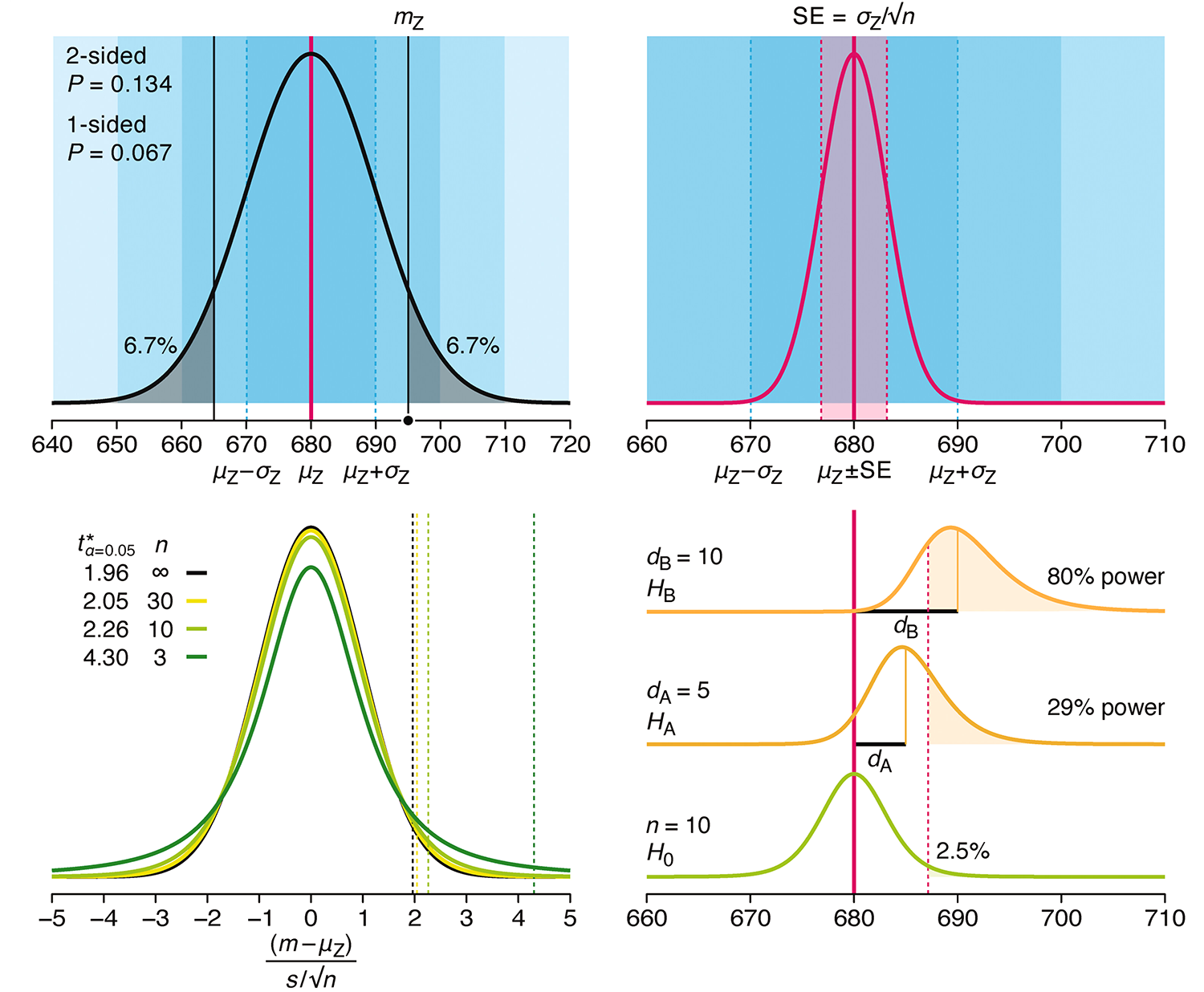
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.

