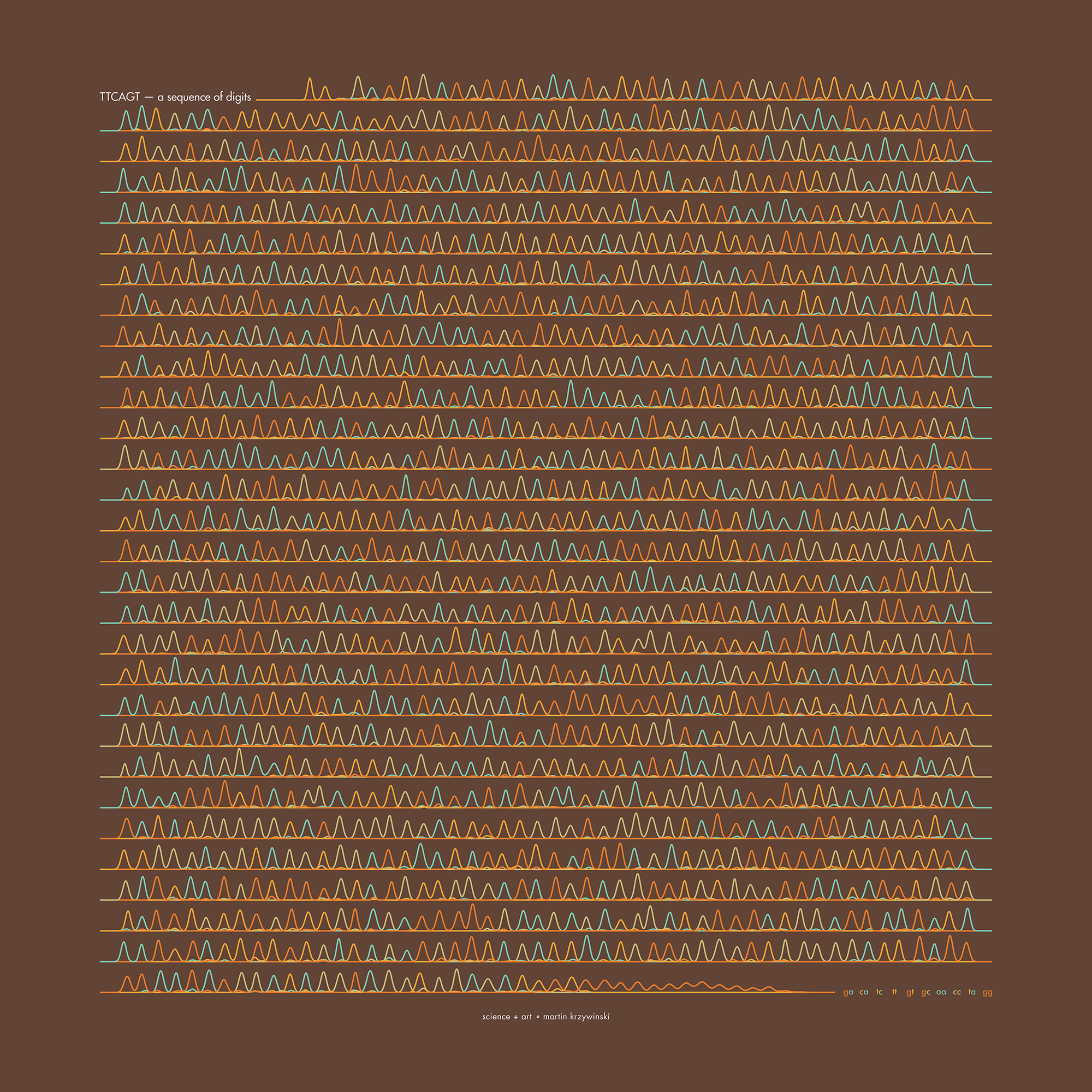 buy artwork
buy artwork
`\pi` Day 2021 Art Posters - A forest of `\pi` (a Lindenmayer system)
On March 14th celebrate `\pi` Day. Hug `\pi`—find a way to do it.
For those who favour `\tau=2\pi` will have to postpone celebrations until July 26th. That's what you get for thinking that `\pi` is wrong. I sympathize with this position and have `\tau` day art too!
If you're not into details, you may opt to party on July 22nd, which is `\pi` approximation day (`\pi` ≈ 22/7). It's 20% more accurate that the official `\pi` day!
Finally, if you believe that `\pi = 3`, you should read why `\pi` is not equal to 3.
The trees along this city street,
Save for the traffic and the trains,
Would make a sound as thin and sweet
As trees in country lanes.
—Edna St. Vincent Millay (City Trees)
 buy artwork
buy artwork
Welcome to this year's celebration of `\pi` and mathematics.
The theme this year is flower and flowers—in contrast to last year's understandable downturn in mood.
This year's `\pi` poem City Trees by Edna St. Vincent Millay.
This year's `\pi` day song is Sway by Laleh.
In past years, I've used the digits to draw a star map, run a gravity simulation draw a star map, draw streets of imagined cities. I even took a stab at waxing poetic.
Play time isn't over. This year, the digits of `\pi` sprout an infinite and irrational forest.
Good things grow for those who wait.
Can you see the digits through the forest?
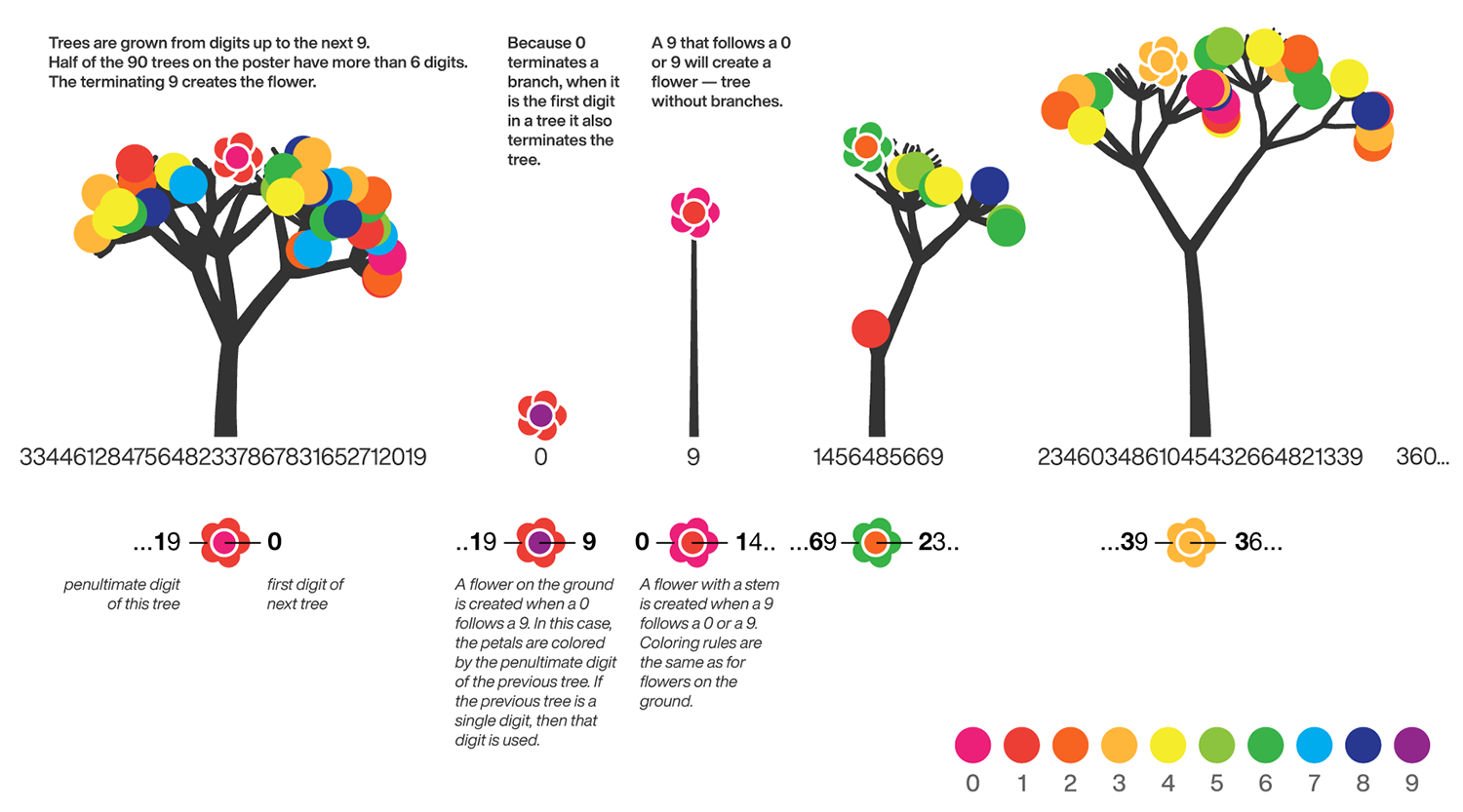
The digits of `\pi` are shown as a forest. Each tree in the forest represents the digits of `\pi` up to the next 9. The first 10 trees are "grown" from the digit sets 314159, 2653589, 79, 3238462643383279, 50288419, 7169, 39, 9, 3751058209, and 749.
The digits control how the tree grows — but there is also a good amount of botanical variation. Below I outline the growth process — see the methods section for details.
the rules of the forest
branches
The first digit of a tree controls how many branches grow from the trunk of the tree. For example, the first tree's first digit is 3, so you see 3 branches growing from the trunk.
The next digit's branches grow from the end of a branch of the previous digit in left-to-right order. This process continues until all the tree's digits have been used up.
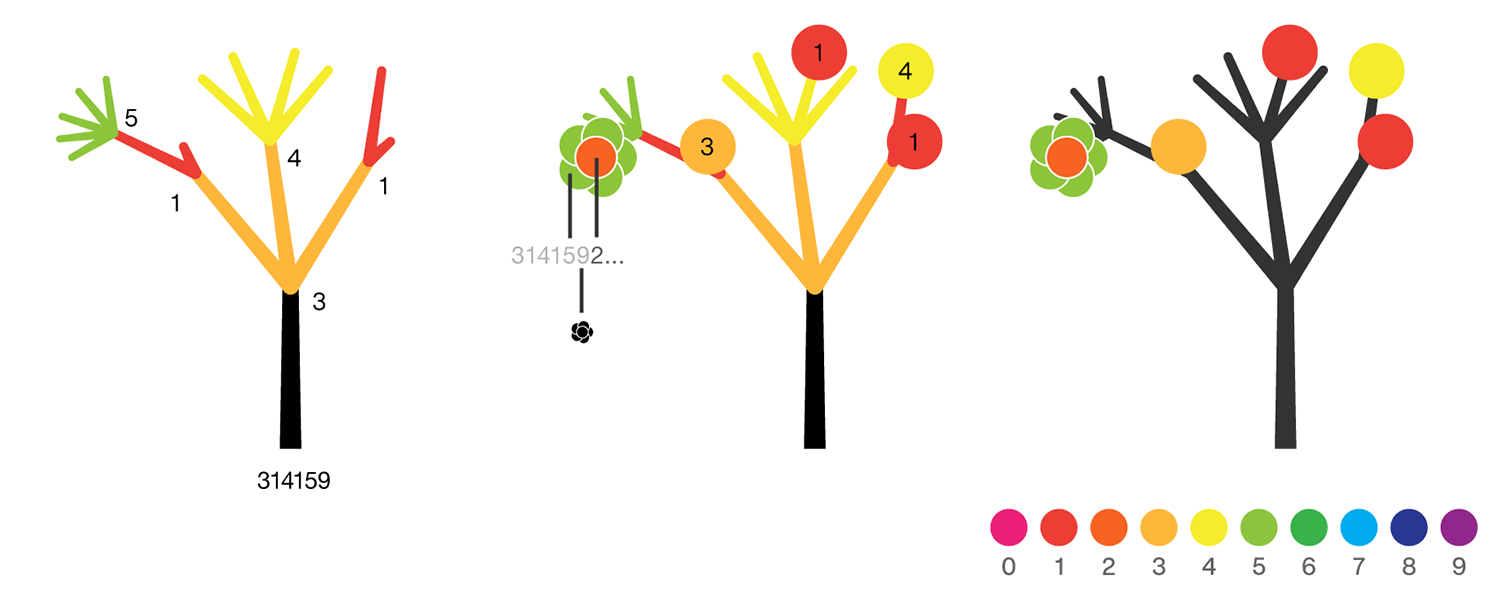
The branching exception is 0, which terminates the current branch — 0 branches grow!
leaves and flowers
The tree's digits themselves are drawn as circular leaves, color-coded by the digit.
The leaf exception is 9, which causes one of the branches of the previous digit to sprout a flower! The petals of the flower are colored by the digit before the 9 and the center is colored by the digit after the 9, which is on the next tree. This is how the forest propagates.
Leaves are placed at the tips of branches in a left-to-right order — you can "easily" read them off. Additionally, the leaves are distributed within the tree (without disturbing their left-to-right order) to spread them out as much as possible and avoid overlap. This order is deterministic.
The leaf placement exception are the branch set that sprouted the flower. These are not used to grow leaves — the flower needs space!
special cases — the forest's children
The digit subset "09" is very special. By the rules above, since 0 terminates the branch and 9 grows a flower, we get a flower on the ground — the tree doesn't get to grow but (luckily) flowers to propagates to the next tree.
Two or more 9's in a row generate a series of flowers. The digit forest poster ends in 5 flowers — these are the Feynman Flowers — created by the 999999 at digit 762, which is called the Feynman Point in `\pi`.
a digit nature walk
The rules of the forest are complicated. The labels below the trees help you orient yourself in the stream of digits. Flowers on the ground have no label.

shhh, the trees are sleeping
When the lights go out, it's harder to tell what's going on.
And if you really want a deep dive, check out the underwater edition.
Sometimes it's cloudy and sad in the forest.
But it's best to see all the posters to make sure you don't miss anything.
How it started
The first digit set is 314159 and the 3141 can be read off from the colored leaves. Left to right, these are: orange, red, yellow, red. The 5 is immediately before a 9, so it sprouts a flower. The petals are colored by the digit (5 is green) and the center by the first digit of the next tree (2 is dark orange).

Some trees are smaller than others. The tree for 79 only has a chance to grow 7 branches from the trunk before sprouting a flower.
How it's going
The artwork shows the forest up to the end of the Feynman Point, which is the first 999999 in `\pi`. It happens at digit 762 and ends at digit 768.

I'll leave you to work out how the Feynman Point results in 5 Feynman Flowers and why the center of the last flower is a different color.
Deterministic but always changing
There is "random" variation in aspects of a tree, such as branch length, angle, and direction of growth. However, the randomness is deterministic — the identical same forest is always generated.
To achieve this, I used the digits of each tree and its predecessor (all but the first have one) to create a random number generator — a linear congruential generator.
If you stare into the forest long enough, you can see the branches sway and sway away.

The more digits in the tree (and its predecessor) the more "randomness" there is in the output of the generator. Two flowers in a row use "99" as the input to the generator, which is no randomness at all. But the generator from the first tree's "314159" offers lots of variation.
Each aspect of the tree that has variation has its own generator. There's more detail about this in the methods section.
Beyond Belief Campaign BRCA Art
Fuelled by philanthropy, findings into the workings of BRCA1 and BRCA2 genes have led to groundbreaking research and lifesaving innovations to care for families facing cancer.
This set of 100 one-of-a-kind prints explore the structure of these genes. Each artwork is unique — if you put them all together, you get the full sequence of the BRCA1 and BRCA2 proteins.
Propensity score weighting
The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)
This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.
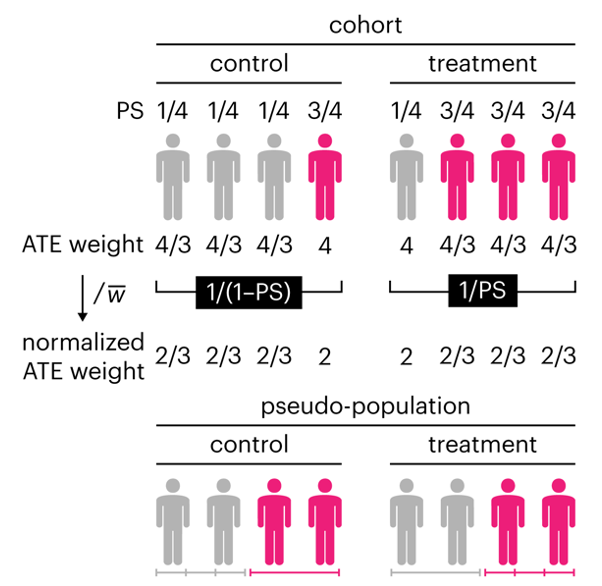
Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.
Happy 2025 π Day—
TTCAGT: a sequence of digits
Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.
Crafting 10 Years of Statistics Explanations: Points of Significance
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.
Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.
In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.
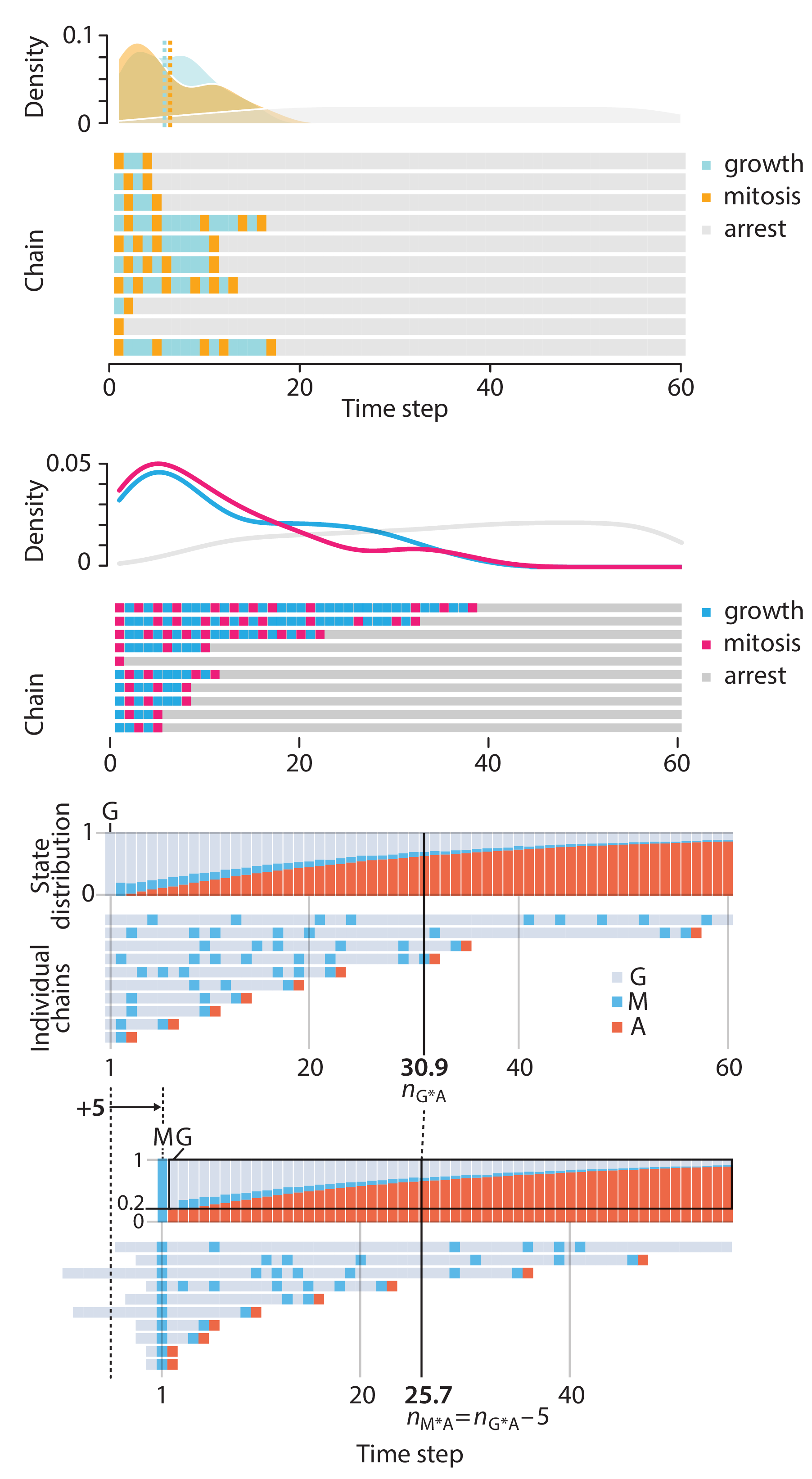
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
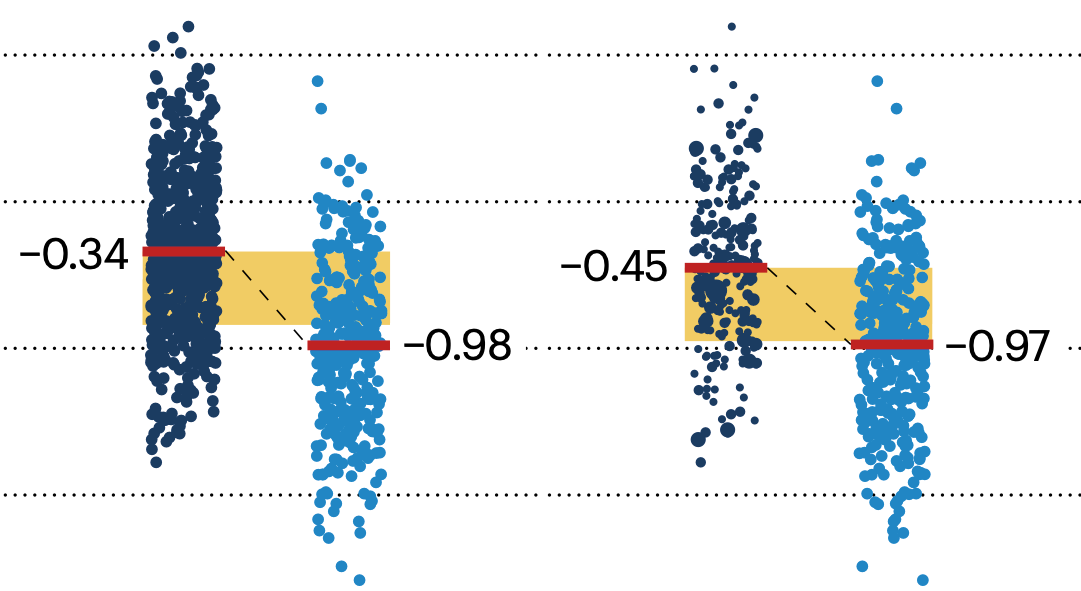
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Understanding p-values and significance
P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.
We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.
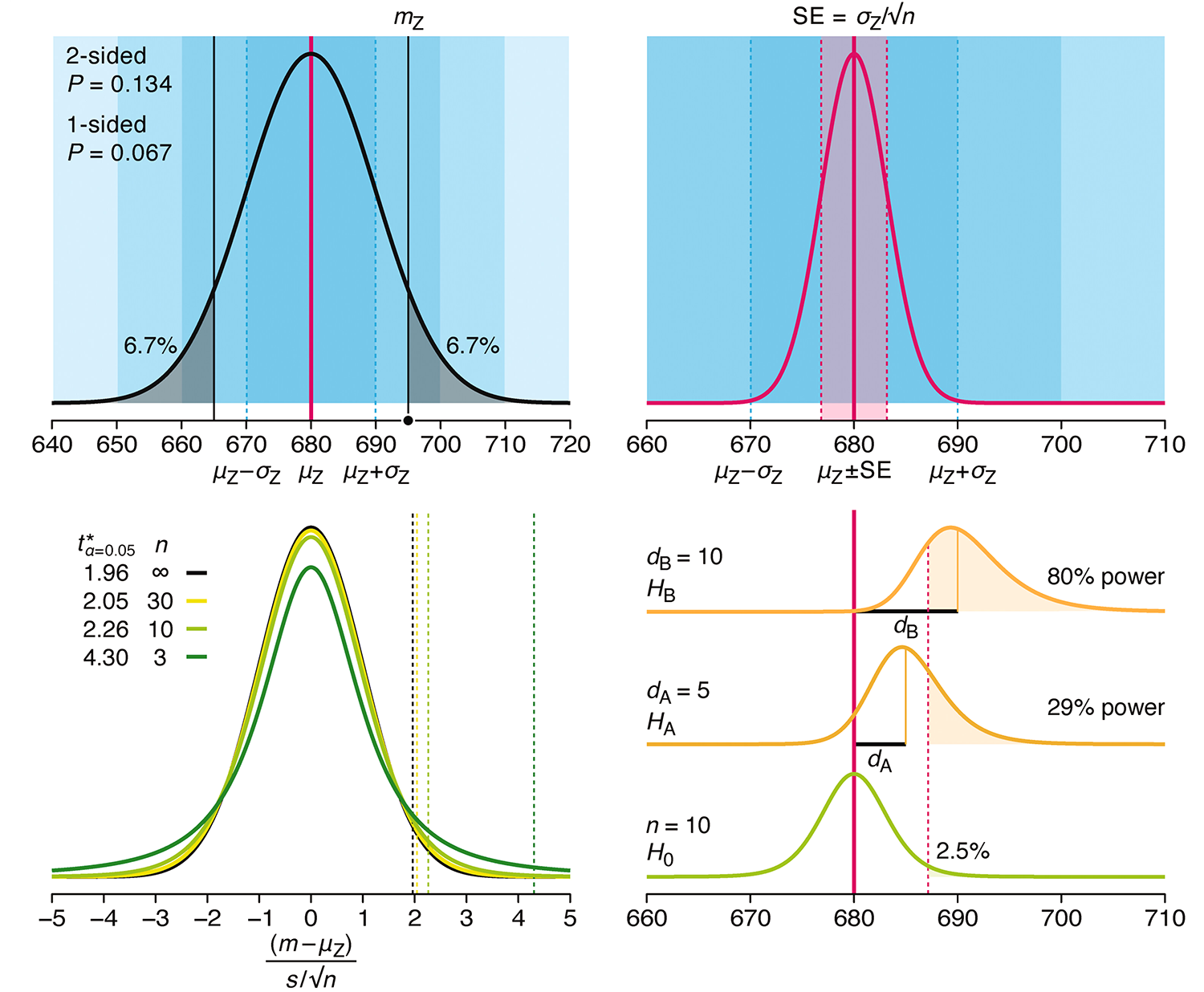
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.