 buy artwork
buy artwork
Pi Day 2023 — Repeated Sequence — A modular synthesizer experience
On March 14th celebrate `\pi` Day. Hug `\pi`—find a way to do it.
For those who favour `\tau=2\pi` will have to postpone celebrations until July 26th. That's what you get for thinking that `\pi` is wrong. I sympathize with this position and have `\tau` day art too!
If you're not into details, you may opt to party on July 22nd, which is `\pi` approximation day (`\pi` ≈ 22/7). It's 20% more accurate that the official `\pi` day!
Finally, if you believe that `\pi = 3`, you should read why `\pi` is not equal to 3.
People find these numbers inconceivable — and I do too. Best thing to do is just relax and enjoy it. —Richard Feynman
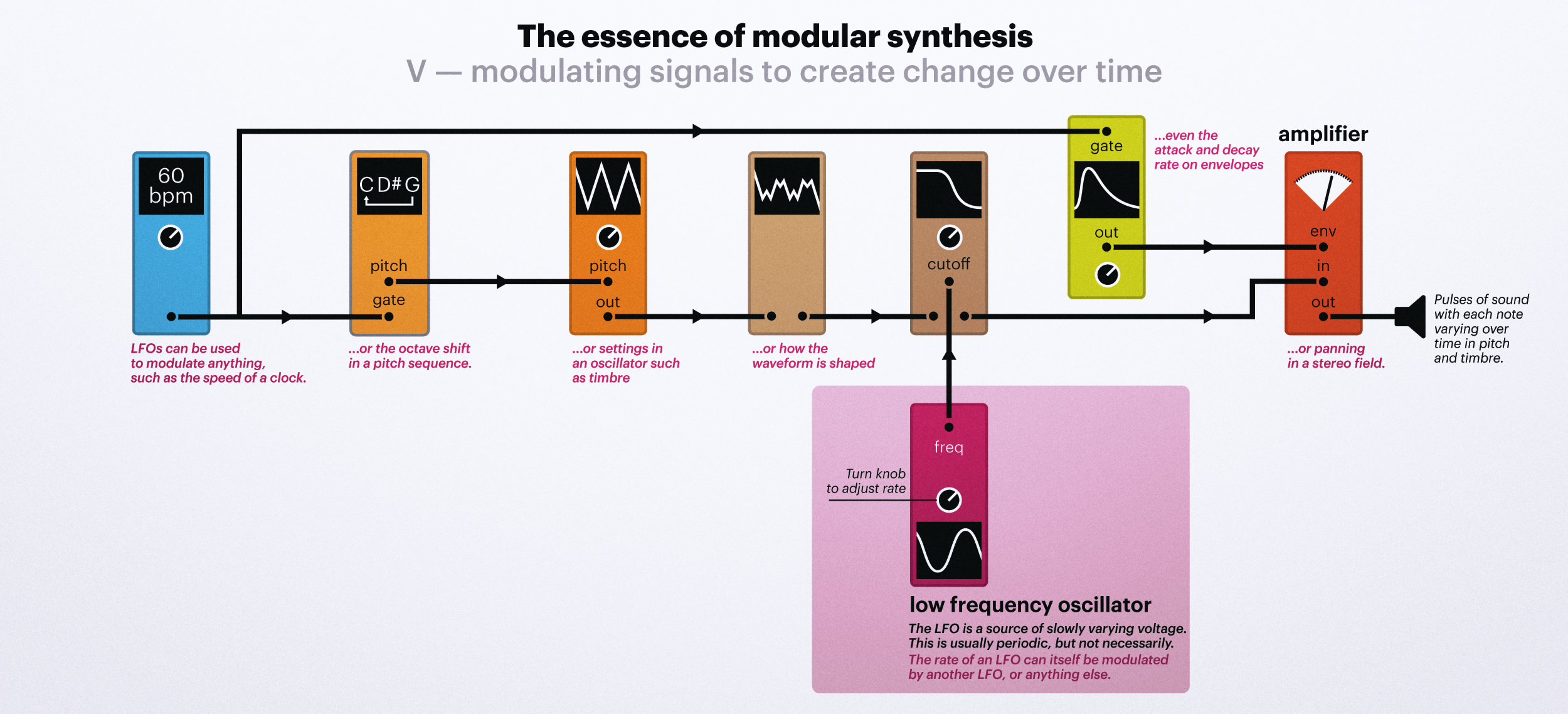
Welcome to 2023 Pi Day: a celebration of `\pi` and mathematics, electronic music and cables. A lot of cables.



contents
This piece was created with a modular synthesizer system, which you can see in the video. Look for the closeups to meet some of the key modules in the patch, such as Vector Space and the Triple Sloths.
You've probably seen at least one synthesizer — most have a keyboard, which allow you to select a note, and they all have a bunch of knobs, which allow you to shape the sound giving you wide control over what a note will sound like. This latter process is broadly known as sound design.
If you were to open up such a synthesizer, you'd see a bunch of different circuits hooked up to the knobs, with each circuit having a specific role in the signal flow. This is a simplification, but it's good enough.
In a modular synthesizer, those individual circuits are broken up into modules that you purchase separately. Each module has its own function — everything from making a sound to filtering to mixing and more. It's probably best to call such a setup a modular system since it can veritably act as multiple synthesizers, each composed of a group of modules.
The modules themselves come in a wide variety of designs and sizes. Some modules are very narrow and some are very wide, though the height of the module is fixed within a given modular standards. For example, Eurorack modules are 5.25" in height (3U, 1U = 1.75") whereas the Buchla/Serge system uses 4U (7") and Moog modular synth modules are 8.75" tall. There are even some short 1.75" (1U) modules in the Eurorack world.
The Triple Sloth is chaos circuit module. It output is the solution to a system of differential equations, similar to the Lorentz System.
There are three sloths, called Torpor, Inertia and Apathy. These have periods of about 20 seconds (Torpor), 2 minutes (Apathy) and 20 minutes (Inertia). You can see the realtime output of the Inertia slot at this point in the video.
There's also a much slower sloth — Sloth DX — with a 20 hour period. This Sloth DX has capacitors that are so large that they stick out from the front of the module. As far as I know, this is the only module that exposes is internal components in this way.
This is a much longer version of the original 1 hour Repeated Sequence, which only went to the Feynman Point (769 digits).
In the 10 hour version we go to 10,000 digits. Up to the Feynman Point, this longer version is identical to the 1 hour version. After this point, though, it just keeps going — we let the modular patch play itself. During this time, we switch reels on the Morphagene to Esther and Anja giggling. There's mumbling too.
Starting at 8,000 digits, we ramp up the rack to a finale at 10,000 digits and then ramp down the rack for an outro. The last ~1,500 digits are read out at 4 digits per second in about 6 min 15 seconds.
If you'd like to learn the basics of modular synthesis, check out the Methods section.
Beyond Belief Campaign BRCA Art
Fuelled by philanthropy, findings into the workings of BRCA1 and BRCA2 genes have led to groundbreaking research and lifesaving innovations to care for families facing cancer.
This set of 100 one-of-a-kind prints explore the structure of these genes. Each artwork is unique — if you put them all together, you get the full sequence of the BRCA1 and BRCA2 proteins.
Propensity score weighting
The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)
This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.
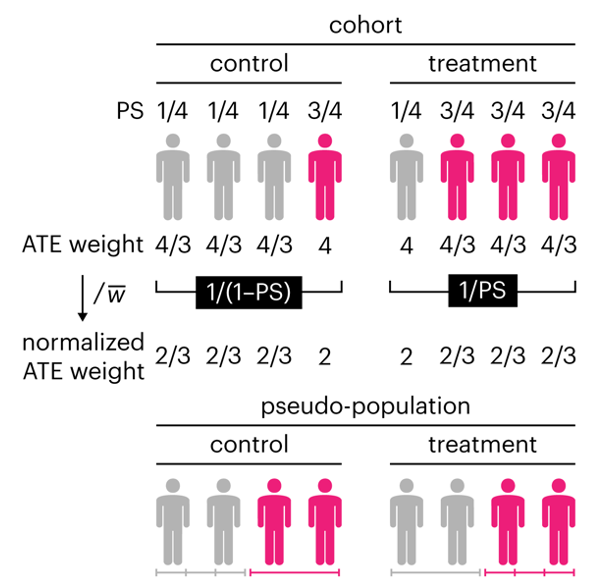
Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.
Happy 2025 π Day—
TTCAGT: a sequence of digits
Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.
Crafting 10 Years of Statistics Explanations: Points of Significance
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.
Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.
In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.
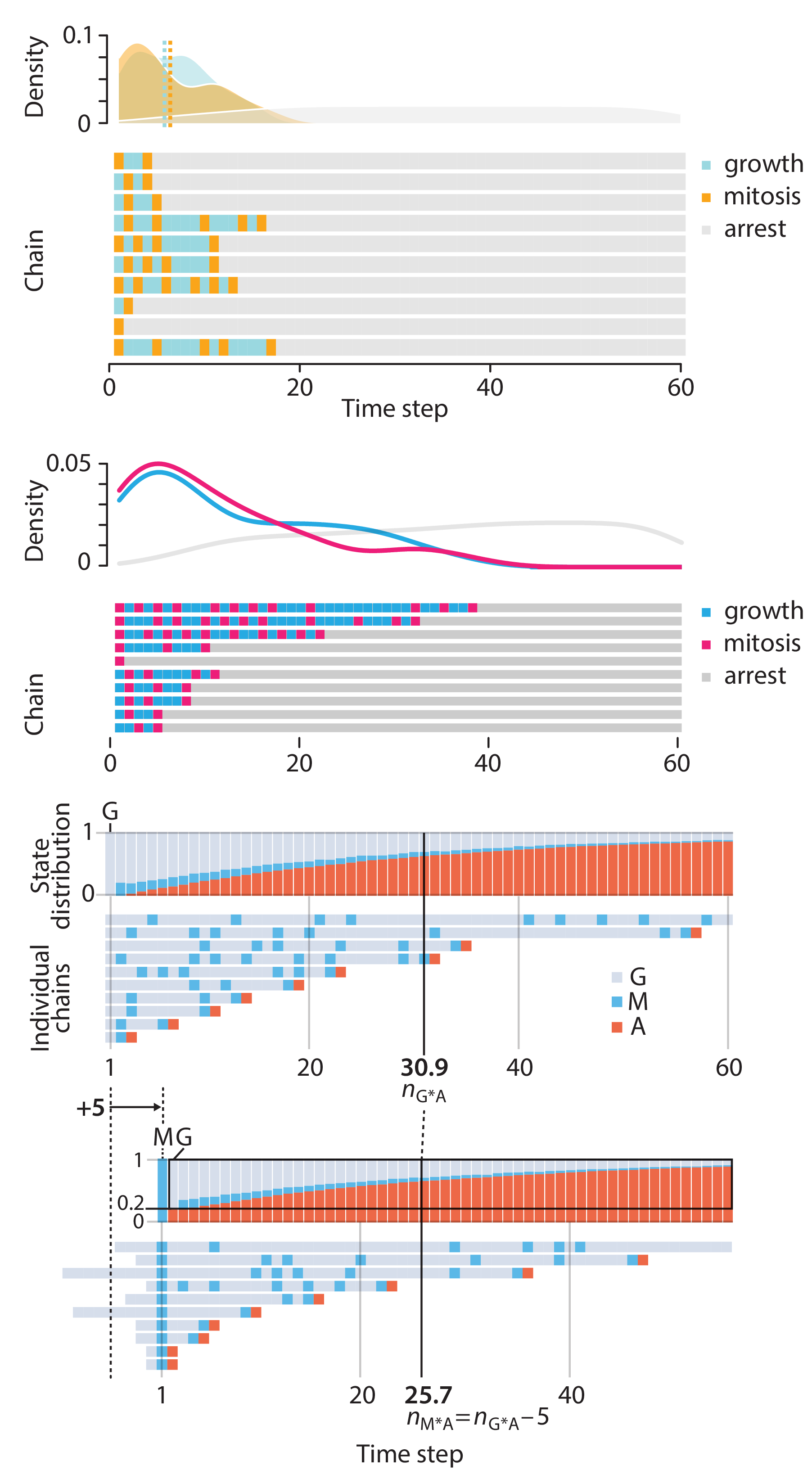
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
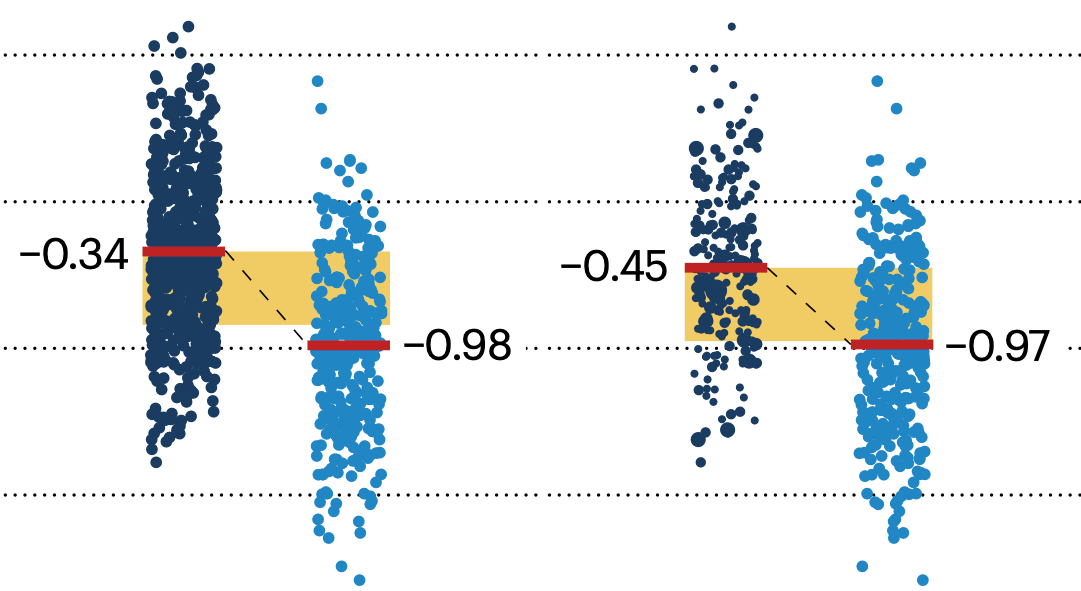
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Understanding p-values and significance
P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.
We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.
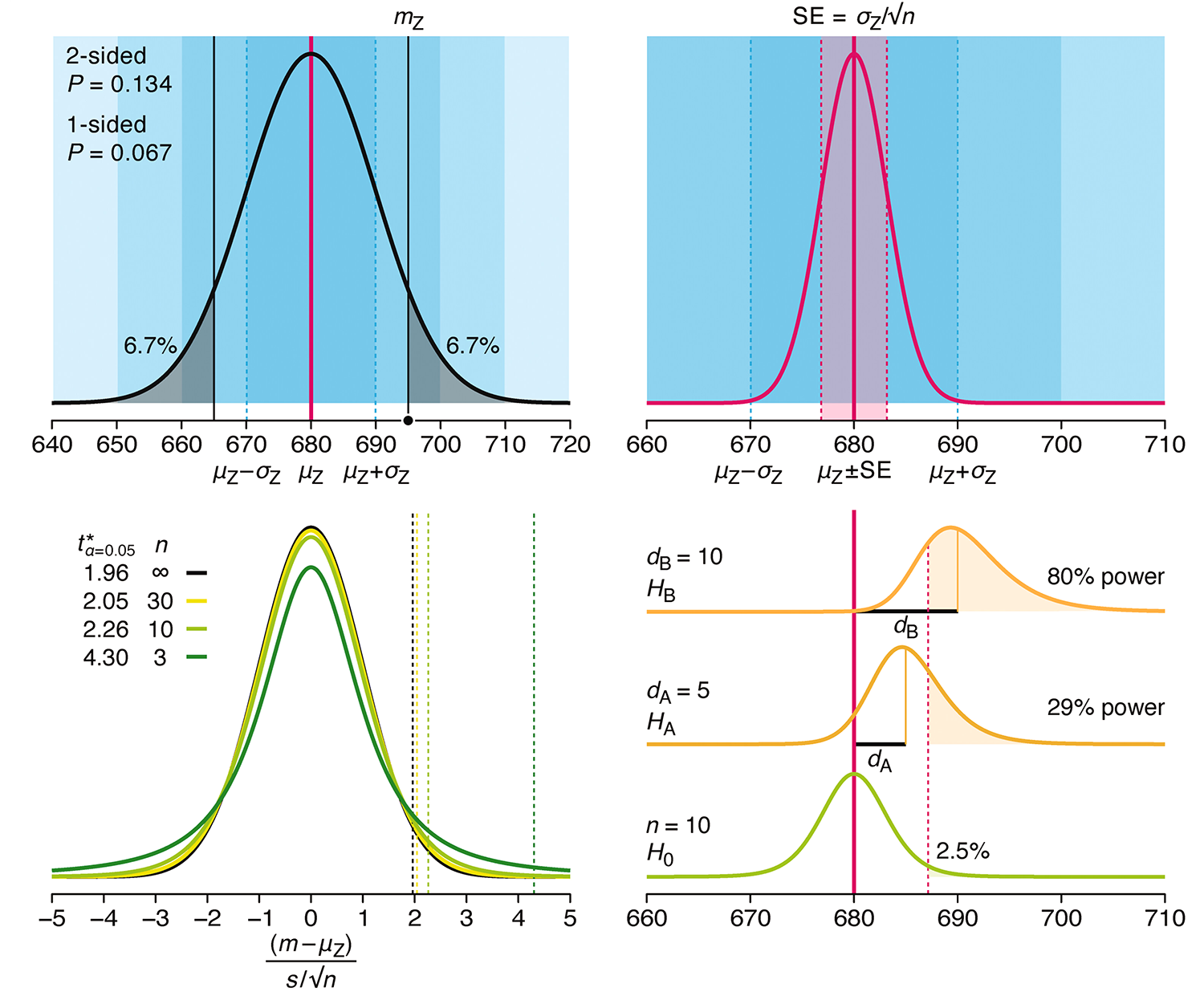
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.