EMBO Journal 2011 Cover Contest
contents

For its 6 May 2009 issue, the EMBO Journal selected my submission of a large Circos figure for its cover. At the time, front page exposure of this sort has made Circos a very popular tool for visualization in genomics, and in particular, in cancer research where there is a need to illustrate differences between genomes.
Below I describe a couple of subsequent submissions for the EMBO Journal 2011 Cover Contest — a scientific entry and a non-scientific entry.
For the EMBO Journal 2011 Cover Contest, I prepared two entries, one for the scientific category and one for the non-scientific category.

The EMBO Journal non-scientific cover prize is awarded for the most interesting and beautiful image made outside the lab. Contestants may submit, for example, photos or artistic impressions of wildlife animals, plants or landscapes. Particularly welcome will also be hand or computer-generated paintings or drawings (or photographs of other works of art) related to a biological or molecular biological topic.
The EMBO Journal scientific cover prize is awarded for the most captivating and thought-provoking contribution depicting a piece of molecular biology research. Entries can include light or electron micrographs, 3D reconstructions or models of biological specimen or molecules, spectacular artefacts collected in the lab, original new views of lab equipment (but not of colleagues!), or other research-based images to be of interest to molecular biologists.


A large number of layout algorithms already exist to attempt to visualize networks. In an attempt to create attractive layouts, node and edge positions are optimized to minimize some fitness function, such as overlap or force (if edges are treated as springs). Unfortunately, as a result it is impossible to relate the position of a node (or the distance between any two nodes in the layout) to their connected neighbourhood in the network. This particularly holds for large networks, where nodes and edge overlap in the layout is unavoidable.
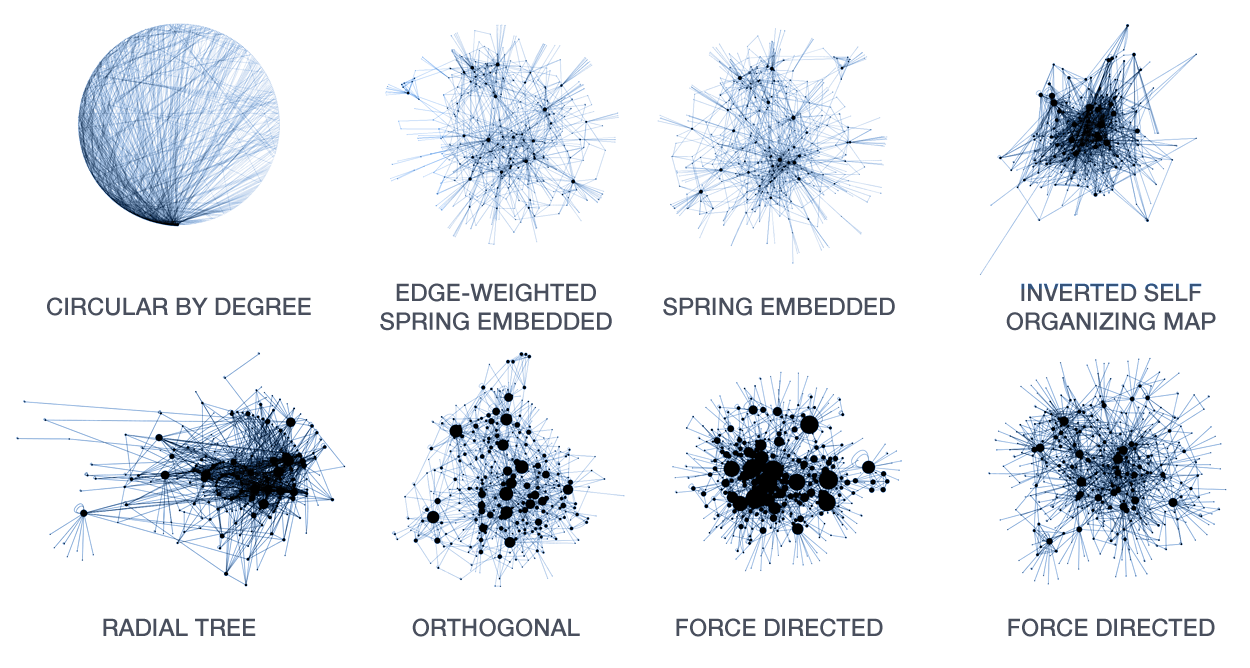
The hive plot is a rational approach to visualizing networks. It is designed to complement (at times, replace) the network hairball.
In a hive plot, network nodes are assigned to and placed on axes using rational rules. These rules typically are a function of local network structure around the node (connectivity, density, centrality, etc). The resulting plot is interpretable.
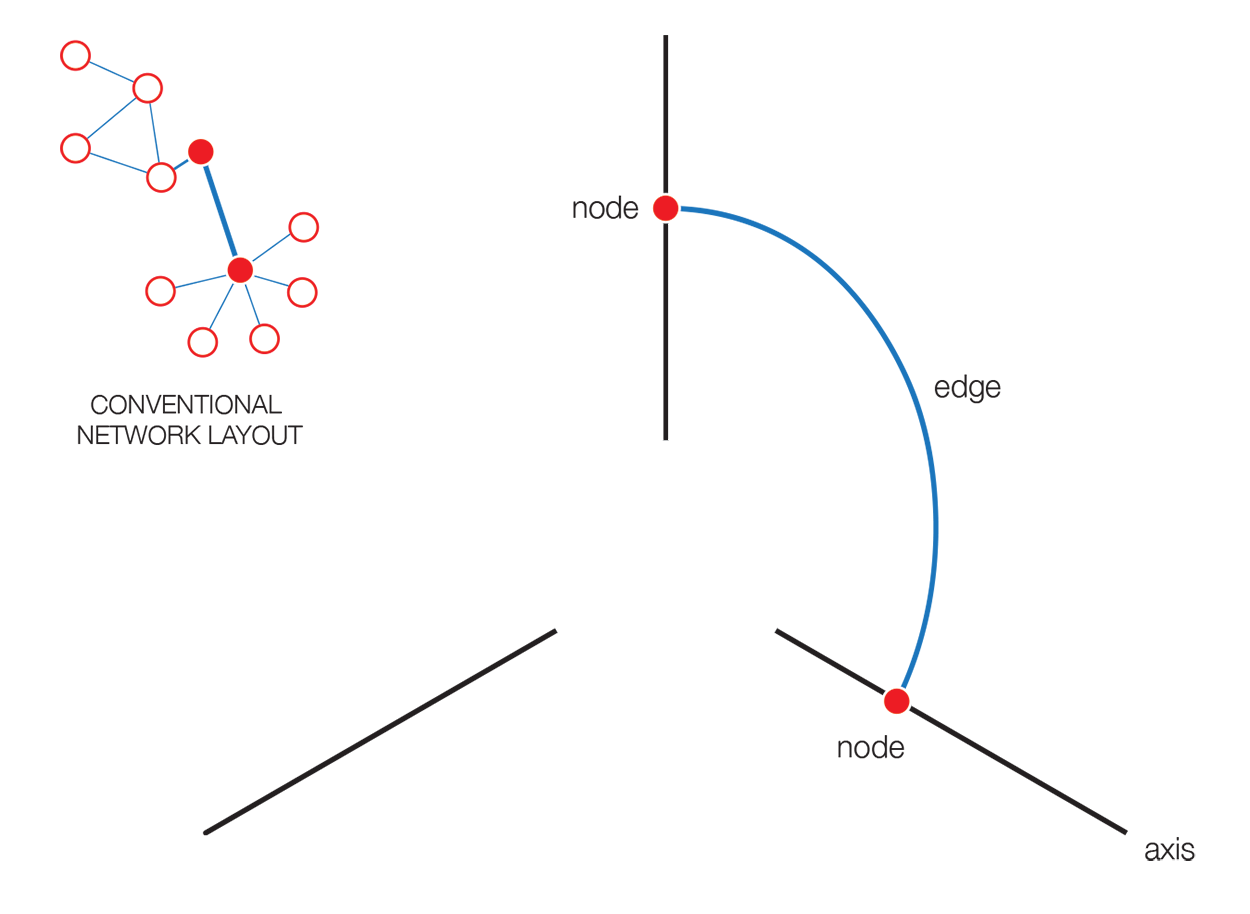
The hive plot can be applied to visualize a large number of ratios between three or more scales.
Instead of network edges, the lines in a hive plot now correspond to an (x,y) data pair, which can be interpreted as a ratio (x/y). This approach is particularly effective when lines are drawn as ribbons, which are then stacked. This is shown in the figure below.
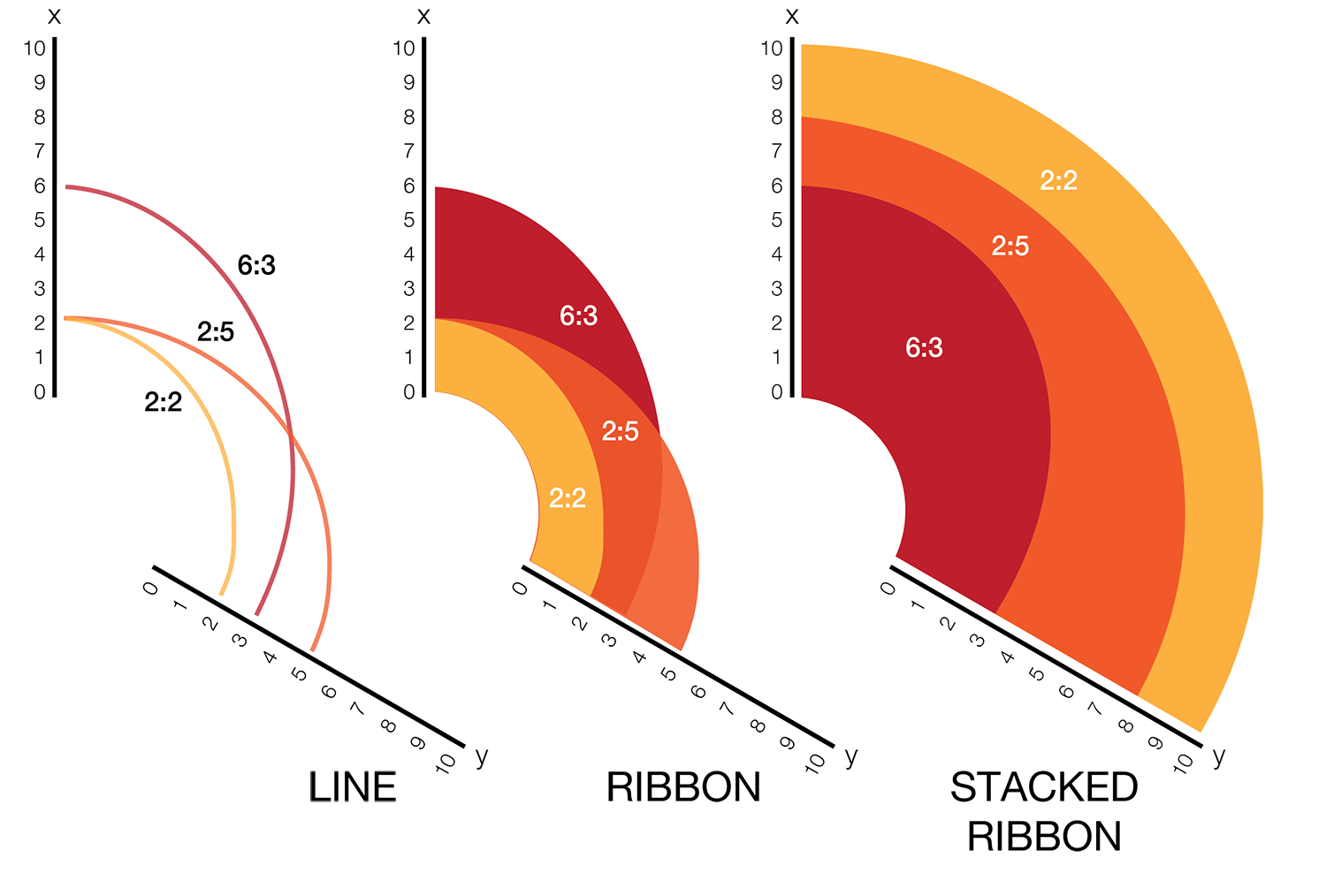
The resulting visualization bears resemblance to a stacked bar plot. The circular layout grants the advantage of being able to instantly compare all pair-wise comparisons between the axes (when three axes are used). This layout also gives the image a compare compact feel and is particularly suitable for tiling.
In the examples below, a 3-axis hive plot is shown with 8 ratios between each axis. The ratios are independent, in the sense that corresponding ribbons (e.g. blue) may have different thickness on either side of an axis. For example, if x:z = 2:3 and x:y = 1:3 then the ribbon on the left of the x axis will be twice as thick as on the right (see black arrow in figure below).
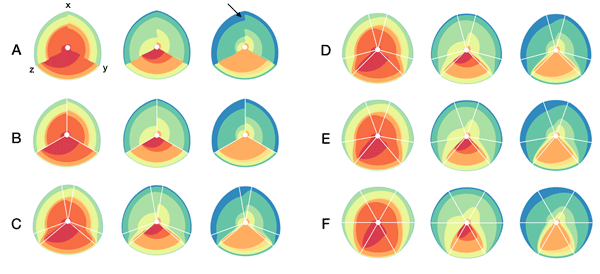
The axes in a hive plot can be arranged arbitrarily. In the figure above panels A and B show 24 ratios — 8 each between x/y, x/z, and y/x axes. In panels C-F each axis is split to create a single 6-axis plot from a dual 3-axis plot. The split axes reveal the transition between ribbons from the left and right sides.
The dual 3-axis plot appears more stylized and mathematical, whereas the single 6-axis plot is softer and organic. As the axis split distance is increased, the plots begin to look like surface density maps, which to some degree occludes the relationships between the ratio ribbons.
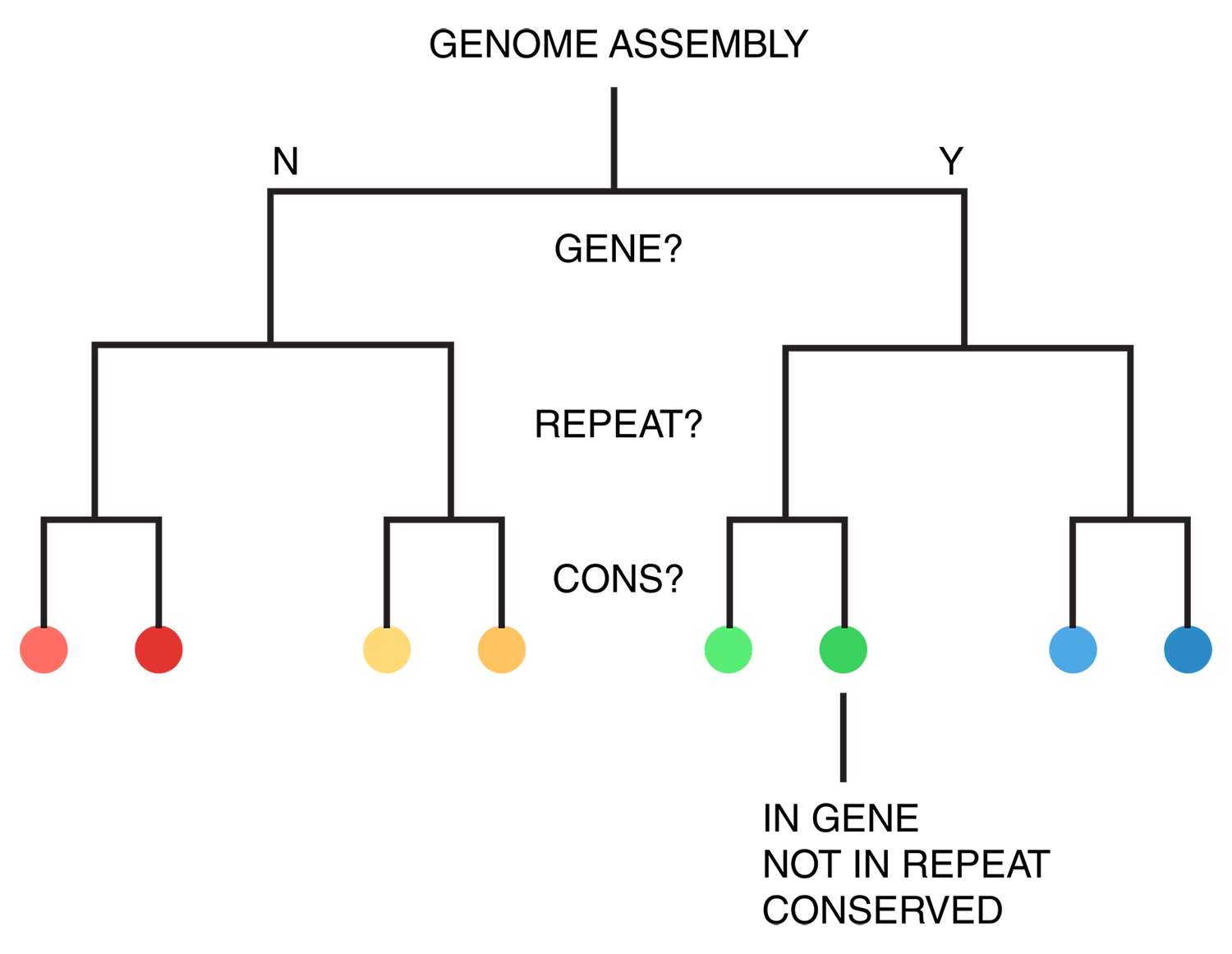
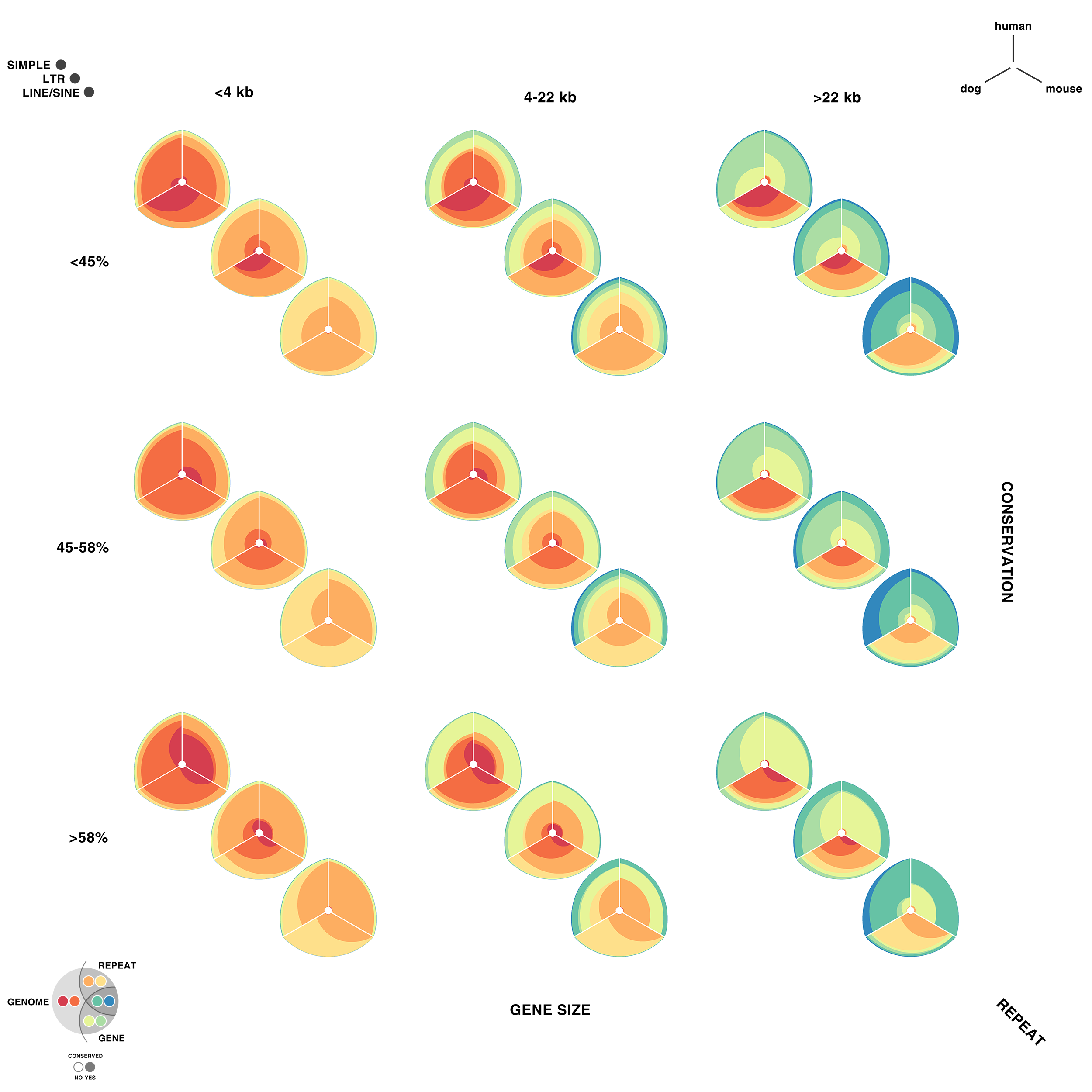
For each of human (hg18), mouse (mm8) and dog (canfam2) genome assemblies, UCSC annotations, available for each genome from the table browser, were used to hierarchically organize each base in the assembly using the following criteria: gene, repeat and gene+repeat. For each of these, bases were further categorized as conserved or not.
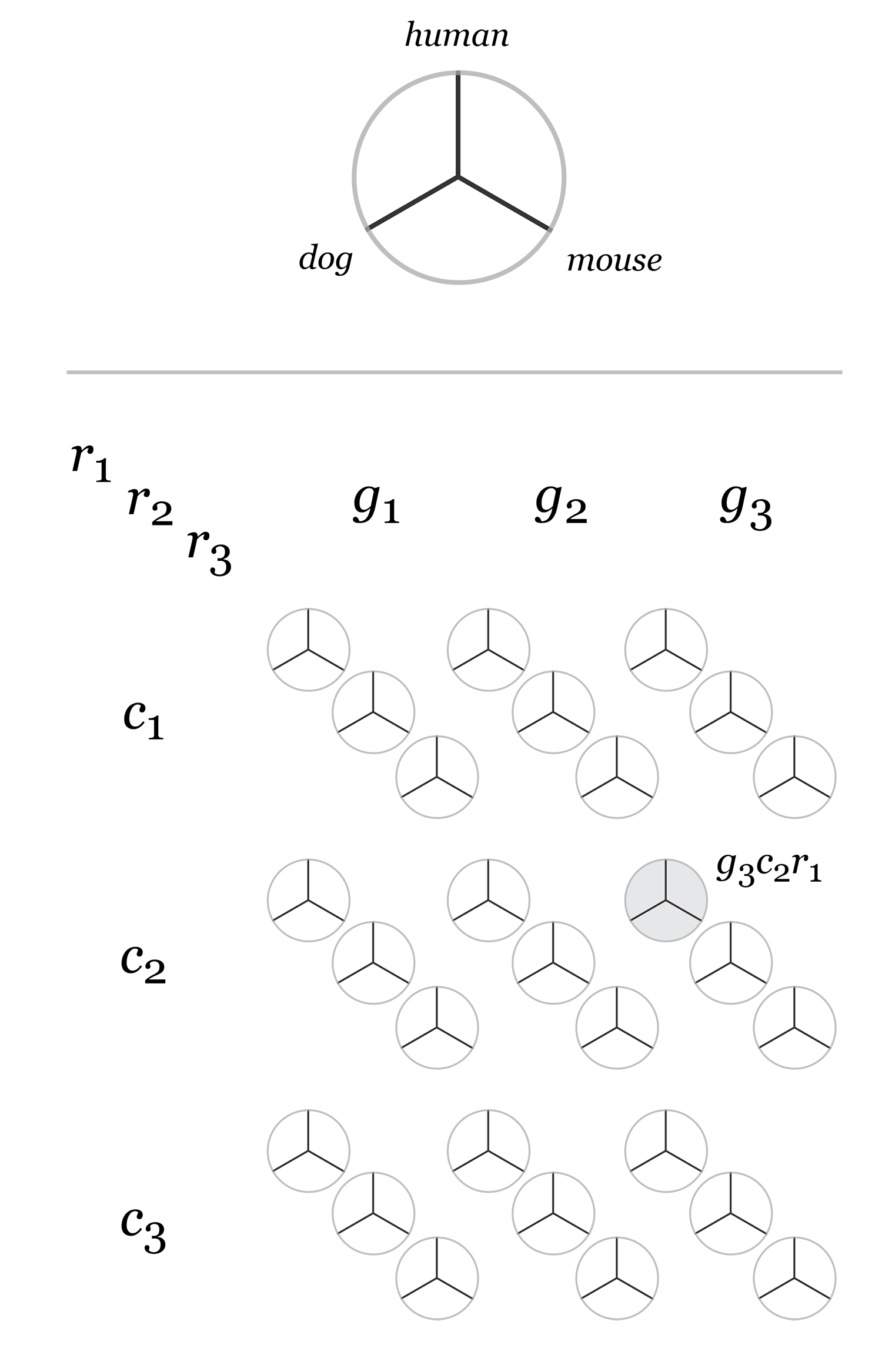
By exhaustively intersecting each of the annotation regions, the assembly was divided into disjoint segments, each with its annotation states. For example, below are a few adjacent regions from hg18 chr1 (a assembly, r repeat, c-cf conserved with dog, c-mm conserved with mouse).
... hg 1 120,942,663 120,945,658 2,996 a r hg 1 120,945,659 120,945,665 7 a hg 1 120,945,666 120,947,239 1,574 a c-cf c-mm hg 1 120,947,240 120,947,243 4 a c-cf c-mm r hg 1 120,947,244 120,947,268 25 a c-mm r hg 1 120,947,269 120,950,367 3,099 a r hg 1 120,950,368 120,950,386 19 a ...
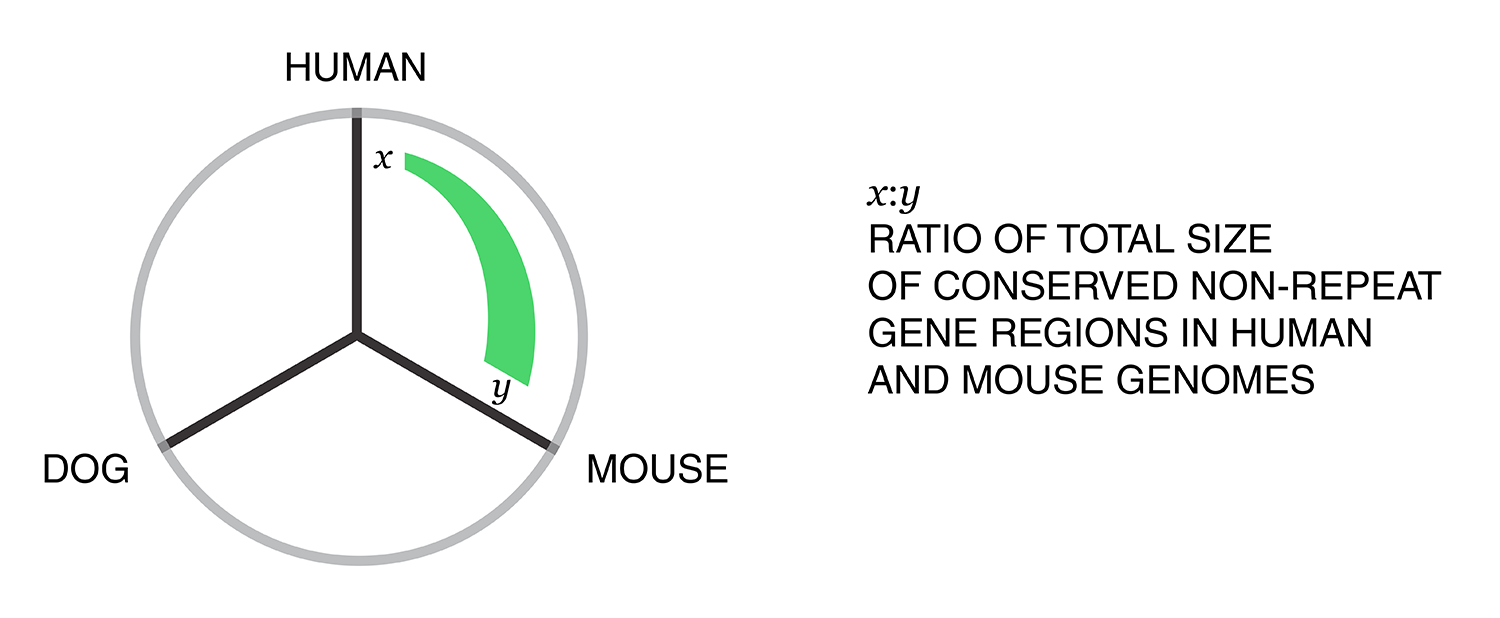
Next, the total size of regions for each combination of annotation was calculated for each pairwise combination of genomes. The second genome in the pair dictates which conservation is used. For example, for the human-mouse pair, the relative fractions of the human genome that fall into each of the categories are
hg mm a 1,839,255,050 0.643542044483869 hg mm a,c-mm 757,027,260 0.264878365091574 hg mm a,r 206,719,589 0.0723296896425132 hg mm a,c-mm,r 42,358,464 0.0148209203088807 hg mm a,g 8,139,587 0.00284798264342638 hg mm a,c-mm,g 4,435,658 0.0015520046651231 hg mm a,g,r 48,994 1.71426463814481e-05 hg mm a,c-mm,g,r 33,869 1.18505182327074e-05
thus categorizing all the 2.86 Gb of the assembled human genome. The corresponding ratios for the mouse genome are
mm hg a 1,388,193,028 0.544355712823795 mm hg a,c-hg 892,892,218 0.350132128602082 mm hg a,r 196,173,508 0.0769260237089193 mm hg a,c-hg,r 62,305,053 0.0244318411447455 mm hg a,g 6,377,904 0.00250098394691097 mm hg a,c-hg,g 4,076,727 0.00159861747416369 mm hg a,g,r 81,889 3.21113447973805e-05 mm hg a,c-hg,g,r 57,585 2.2580954586784e-05
Using these two lists, all the ratios between the human and mouse axes can be determined. For example, for the conserved/gene/non-repeat regions the ratio of human:mouse is 0.00155:0.00160 (lines are bolded above). The corresponding ribbon for this ratio is shown below.
Category assignment into repeat, gene and conserved region was parametrized into three ranges for each criteria. These values were selected heuristically, to obtain a reasonable sample for each combination.
- gene g1 <4kb, g2 4kb-22kb, g3 >22kb
- repeat r1 simple, r2 LTR, r3 LINE/SINE
- conservation c1 <45%, c2 45%-58%, c3 >58%
Given 3 parameters for each of the categories, the full comparison is represented by 27 hive plots. These plots are arranged on the cover as follows
The scale of the axes was logarithmic to maintain visibility of all categories.
My 2011 non-scientific fiber optic entry received an honorouable mention. Oh well, we can't always have nice things.
Some time ago, I photographed fiber optic strands. These worked out well. I had not done anything with these images, and thought they would make a competitive entry into the cover contest.

I revisited the fiber optic lamp with a higher resolution camera (Canon 5D — original images were from a Canon 20D) and a dedicated macro lens (Sigma 150mm f2.8 EX APO DG HSM Macro) (original images were shot with the Canon EF 24-70L).
From these new images, shown below, I created five EMBO Journal cover submissions.

The submissions would render on the cover as shown below.





Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
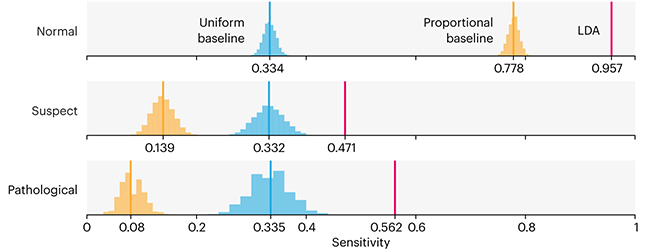
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance5, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 20.
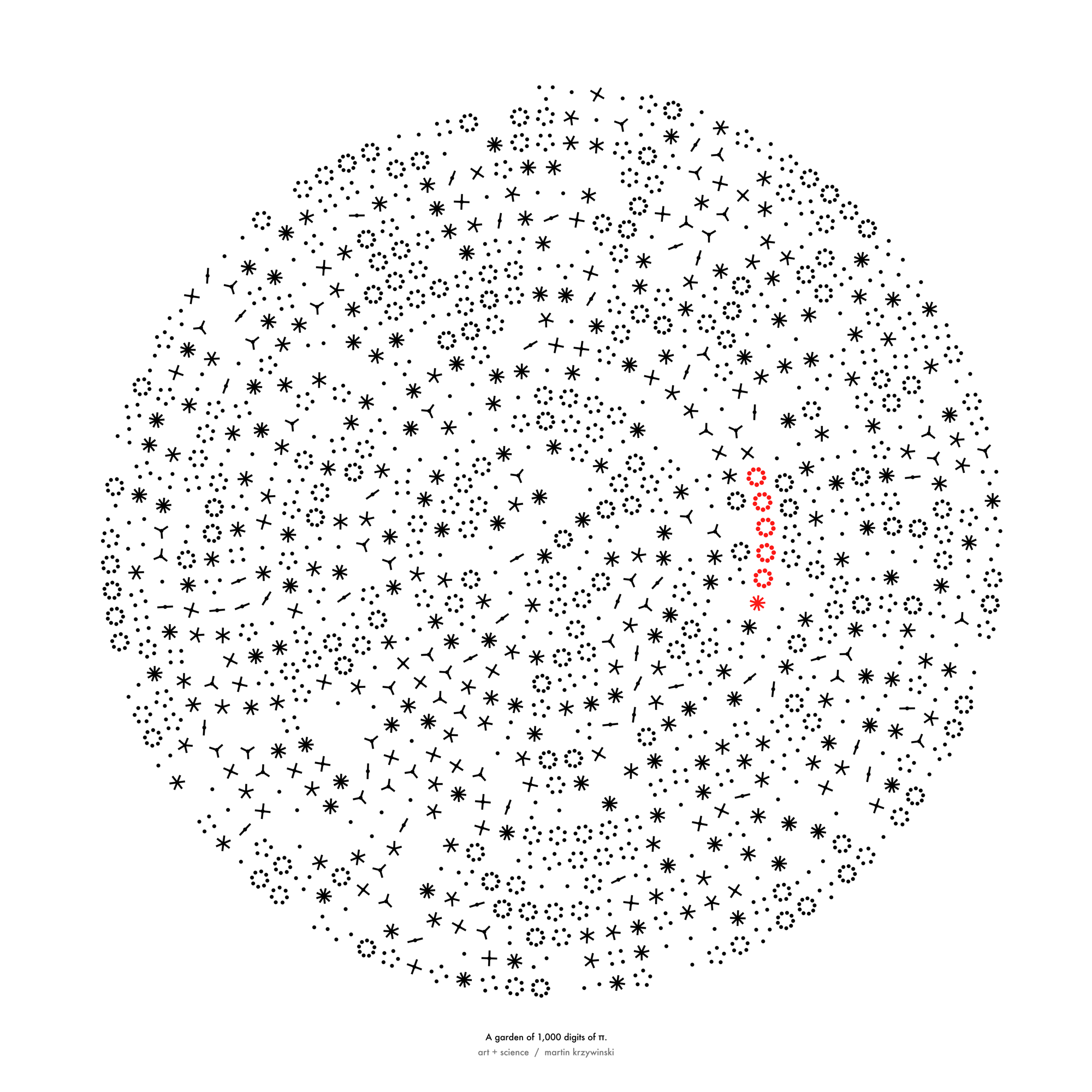
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology
Error in predictor variables
It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible. —Aristotle
In regression, the predictors are (typically) assumed to have known values that are measured without error.
Practically, however, predictors are often measured with error. This has a profound (but predictable) effect on the estimates of relationships among variables – the so-called “error in variables” problem.
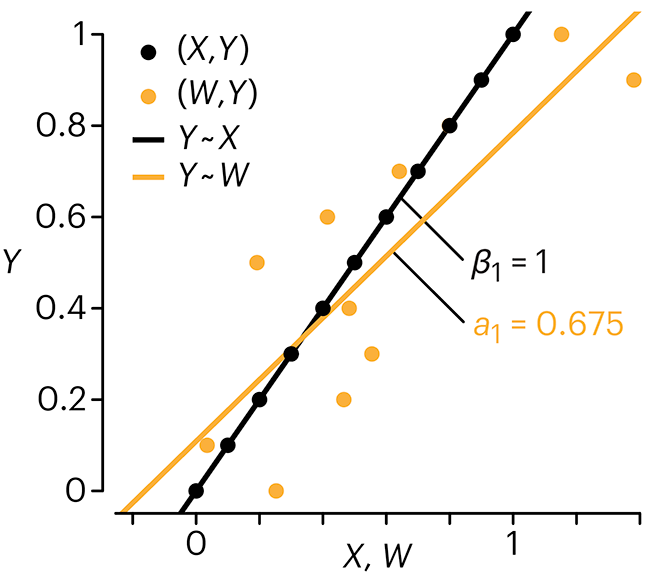
Error in measuring the predictors is often ignored. In this column, we discuss when ignoring this error is harmless and when it can lead to large bias that can leads us to miss important effects.
Altman, N. & Krzywinski, M. (2024) Points of significance: Error in predictor variables. Nat. Methods 20.
Background reading
Altman, N. & Krzywinski, M. (2015) Points of significance: Simple linear regression. Nat. Methods 12:999–1000.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nat. Methods 13:541–542 (2016).
Das, K., Krzywinski, M. & Altman, N. (2019) Points of significance: Quantile regression. Nat. Methods 16:451–452.
Convolutional neural networks
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry. – Richard Feynman
Following up on our Neural network primer column, this month we explore a different kind of network architecture: a convolutional network.
The convolutional network replaces the hidden layer of a fully connected network (FCN) with one or more filters (a kind of neuron that looks at the input within a narrow window).
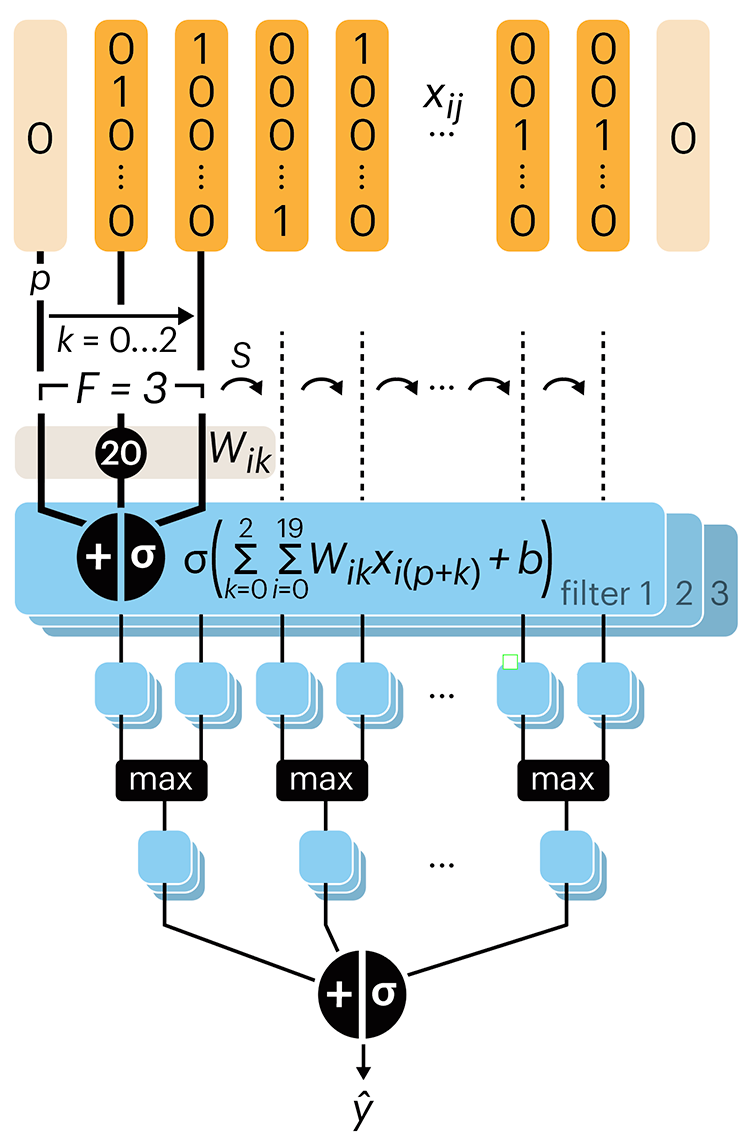
Even through convolutional networks have far fewer neurons that an FCN, they can perform substantially better for certain kinds of problems, such as sequence motif detection.
Derry, A., Krzywinski, M & Altman, N. (2023) Points of significance: Convolutional neural networks. Nature Methods 20:1269–1270.
Background reading
Derry, A., Krzywinski, M. & Altman, N. (2023) Points of significance: Neural network primer. Nature Methods 20:165–167.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nature Methods 13:541–542.