Science Magazine cover — Human Genome Special Issue
The issue explores lessons from past studies of human genomics, with an eye toward future research efforts | 24 September 2021 | Volume 373 | Issue 6562
data sources
1. Amberger JS, Bocchini CA, Schiettecatte FJM, Scott AF, Hamosh A. OMIM.org: Online Mendelian Inheritance in Man (OMIM®), an online catalog of human genes and genetic disorders. Nucleic Acids Research 43:D789–98 (2015).
2. Pleasance E, Titmuss E, Williamson L et al. (2020) Pan-cancer analysis of advanced patient tumors reveals interactions between therapy and genomic landscapes. Nature Cancer 1:452–468.
genome as a spiral
The length of the spiral was chosen so that the scale on the cover is exactly 1,000,000 bases per centimetre. The spiral is given by $$ r = \frac{r_0}{2\pi} \left( 1 - \frac{\theta ^{k}}{n_{\textrm{turns}}} \right) $$
where `r_0 = 490.06321`, `n_{\textrm{turns}} = 60` and `k = 1.01`. The angle starts at `\theta = 0` (corresponds to 12 o'clock in the image) and progresses clockwise until `r = 0`.
The parameter `k` allows me to slightly perturb the rate of winding of the spiral so that the spiral can be of the exact length, all the while fully filling the cover.


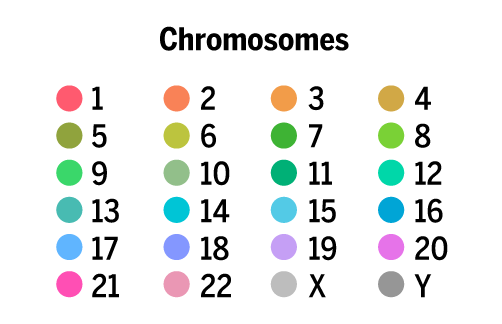
chromosomes
The lengths of the chromosomes in the latest version of the human genome assembly (hg38, December 2013) are as follows.
1 len 248,956,422 clen 248,956,422 2 len 242,193,529 clen 491,149,951 3 len 198,295,559 clen 689,445,510 4 len 190,214,555 clen 879,660,065 5 len 181,538,259 clen 1,061,198,324 6 len 170,805,979 clen 1,232,004,303 7 len 159,345,973 clen 1,391,350,276 8 len 145,138,636 clen 1,536,488,912 9 len 138,394,717 clen 1,674,883,629 10 len 133,797,422 clen 1,808,681,051 11 len 135,086,622 clen 1,943,767,673 12 len 133,275,309 clen 2,077,042,982 13 len 114,364,328 clen 2,191,407,310 14 len 107,043,718 clen 2,298,451,028 15 len 101,991,189 clen 2,400,442,217 16 len 90,338,345 clen 2,490,780,562 17 len 83,257,441 clen 2,574,038,003 18 len 80,373,285 clen 2,654,411,288 19 len 58,617,616 clen 2,713,028,904 20 len 64,444,167 clen 2,777,473,071 21 len 46,709,983 clen 2,824,183,054 22 len 50,818,468 clen 2,875,001,522 x len 156,040,895 clen 3,031,042,417 y len 57,227,415 clen 3,088,269,832
There are other scaffold entries in the assembly file (e.g. chr M and unanchored segments) but these were omitted from the graphic. The mitochondrial chromosome is only 16,569 bp long, which corresponds to only 0.2 mm on the cover.

revenge of the rainbow color palette
The chromosome color palette used in the UCSC genome browser is this

One of the things the original UCSC color palette doesn't get exactly right is luminance normalization. Some colors are very bright (e.g. chr10 yellow) while others are very dark (e.g. chr14 blue). Given that bright elements (generally) command more attention than dark ones, most color palettes for ordinal or nominal variables have some kind of threshold to how much luminance (and chroma) can differ.
Below you can see the UCSC color palette normalized to luminance `L = 70, 80, 90`. While this kind of normalization satisifes some technical requirements for perceptual uniformity, these palettes lack vigor. For strict visualization you probably don't want vigor, but for artistic treatments you probably do.

A while back I looked into generating color palettes of maximally distinct colors. These palettes are formed by clustering all possible colors using perceptually uniform metric (e.g. CIE 2000 `\Delta E`) into `n` clusters. The centroid of each cluster gives the color and, as a set, these centroids are reasonably distributed through color space (e.g. Lab) in such a way that the `\Delta E` between any color and its closest neighbour is roughly the same.
I knew that I was going to make chromosomes X and Y grey, so all I needed were 22 maximally distinct colors for chromosomes 1 – 22. To select these colors, I took all colors in the LCH range `L = [60,80]`, `C = [20,100]` and `H = [0,359]` (all hues) and sampled them every `\Delta L = 5`, `\Delta C = \Delta H = 1`. This yielded 24,928 colors.
picking colors lum 60 ncolors 0 picking colors lum 65 ncolors 5715 picking colors lum 70 ncolors 10975 picking colors lum 75 ncolors 15925 picking colors lum 80 ncolors 20602 initial colors 24928
As I was building the list, any colors within `\Delta E_\textrm{00} < 2` a color already in the list were rejected (to speed up the calculations). This reduced the number of colors to cluster from 24,928 to 6,240.
removing nearby colors within dE00 2 filtering colors 0 nfiltered 0 filtering colors 1000 nfiltered 5159 filtering colors 2000 nfiltered 8600 filtering colors 3000 nfiltered 11024 filtering colors 4000 nfiltered 12728 filtering colors 5000 nfiltered 13947 filtering colors 6000 nfiltered 14958 filtering colors 7000 nfiltered 15673 filtering colors 8000 nfiltered 16261 filtering colors 9000 nfiltered 16698 filtering colors 10000 nfiltered 17084 filtering colors 11000 nfiltered 17442 filtering colors 12000 nfiltered 17697 filtering colors 13000 nfiltered 17891 filtering colors 14000 nfiltered 18037 filtering colors 15000 nfiltered 18147 filtering colors 16000 nfiltered 18269 filtering colors 17000 nfiltered 18346 filtering colors 18000 nfiltered 18428 filtering colors 19000 nfiltered 18483 filtering colors 20000 nfiltered 18541 filtering colors 21000 nfiltered 18584 filtering colors 22000 nfiltered 18624 filtering colors 23000 nfiltered 18657 filtering colors 24000 nfiltered 18679 got 6240 colors
Clustering was done using `k`-means with `\Delta E_\textrm{94}` as the distance metric. It's much faster than `\Delta E_\textrm{00}` and only subtly different.

This color cluster centroids are
# R G B L C H nearest & distance i 0 235 161 135 72 34 46 j 1 dE00 11.64 i 1 255 126 70 68 72 48 j 0 dE00 11.64 i 2 246 158 67 72 64 66 j 3 dE00 12.04 i 3 216 173 84 73 51 83 j 2 dE00 12.04 i 4 187 186 58 73 63 103 j 5 dE00 10.88 i 5 169 184 118 72 35 116 j 4 dE00 10.88 i 6 145 205 64 76 73 123 j 7 dE00 9.54 i 7 88 183 68 66 69 135 j 8 dE00 9.06 i 8 64 214 110 76 73 146 j 7 dE00 9.06 i 9 123 193 144 72 36 151 j 8 dE00 11.02 i 10 0 208 161 73 62 171 j 9 dE00 11.90 i 11 86 195 191 72 32 194 j 12 dE00 12.86 i 12 0 206 221 71 74 201 j 11 dE00 12.86 i 13 79 189 227 72 34 235 j 11 dE00 14.52 i 14 111 176 255 71 51 277 j 15 dE00 13.47 i 15 166 166 249 70 45 295 j 16 dE00 12.71 i 16 210 140 255 70 73 313 j 15 dE00 12.71 i 17 252 123 223 69 67 335 j 18 dE00 11.58 i 18 212 163 219 73 34 323 j 17 dE00 11.58 i 19 243 152 176 72 37 2 j 20 dE00 12.56 i 20 255 83 166 66 78 0 j 17 dE00 12.40 i 21 255 110 117 67 67 24 j 19 dE00 14.34
Each color is indentified by index `i`. Its closest neighbour (in terms of `\Delta E`) is color `j` and the distance between them is `\Delta E_{\textrm{00}}`. You can see that this distance to the nearest neighbour is reasonably constant(ish) (average difference is 12.3).
Note that there are two color pairs with very similar hue (`i = 0,1` and `i = 19,20`).
There are lots of greenish colors — this reflects the fact that green occupies a relatively large part of the color space.
other palette options
It's worth exploring a few different clustering scenarios, which differ by how colors to be clustered are sampled across luminance and chroma. For example, option "I" clusters 2,544 colors sampled from ranges `L = [60,80]` and `C = [80,100]` (very saturated). If we restrict color sampling to a single luminance and chroma, we get something like option "O", which clusters 104 colors with `L = 60` and `C = 80`.
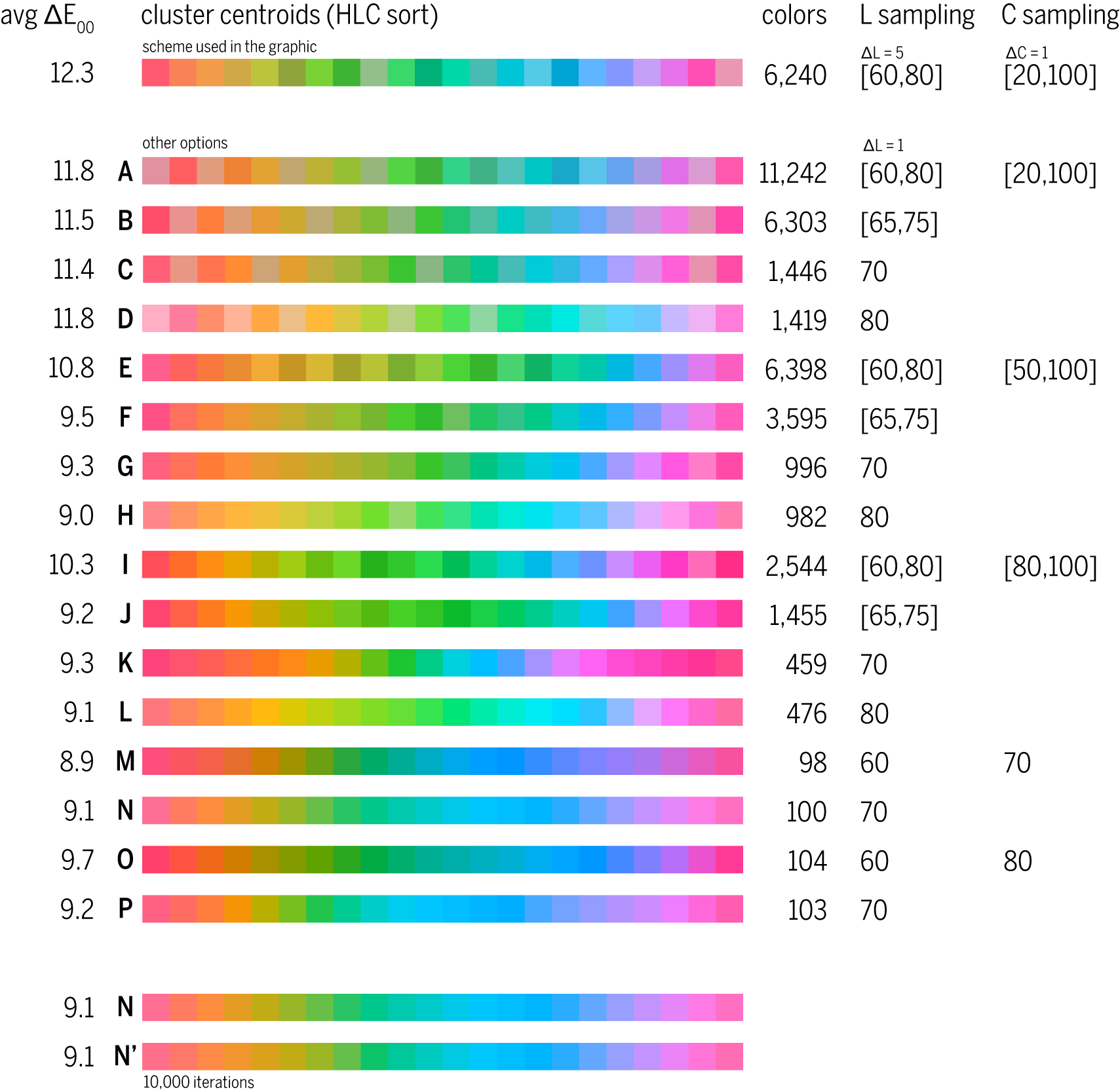
If we want 22 colors that then it's necessary to sample from a variety of luminance and chroma values. Otherwise, colors vary only by hue and some are difficult to discern. For example, in option "N" which samples from fixed `L = C = 70`, the clustering gives
i 0 255 124 98 70 69 37 j 1 dE00 14.25 i 1 255 141 63 70 69 57 j 2 dE00 14.19 i 2 228 157 35 70 69 75 j 1 dE00 14.19 i 3 193 172 21 70 69 95 j 4 dE00 13.21 i 4 151 183 41 70 69 114 j 5 dE00 10.02 i 5 104 191 72 70 69 133 j 6 dE00 7.50 i 6 40 196 101 70 69 148 j 5 dE00 7.50 i 7 0 199 140 70 69 166 j 8 dE00 8.93 i 8 0 201 174 70 69 182 j 9 dE00 7.97 i 9 0 201 202 70 69 195 j 8 dE00 7.97 i 10 0 200 233 70 69 210 j 11 dE00 6.85 i 11 0 198 255 70 69 224 j 10 dE00 6.85 i 12 0 190 255 70 69 249 j 13 dE00 9.47 i 13 0 181 255 70 69 266 j 14 dE00 8.43 i 14 43 173 255 70 69 278 j 15 dE00 5.53 i 15 99 168 255 70 69 285 j 14 dE00 5.53 i 16 152 159 255 70 69 296 j 15 dE00 9.75 i 17 195 147 255 70 69 308 j 18 dE00 8.99 i 18 230 134 251 70 69 322 j 19 dE00 6.60 i 19 254 122 228 70 69 335 j 18 dE00 6.60 i 20 255 112 195 70 69 351 j 19 dE00 7.76 i 21 255 110 148 70 69 12 j 20 dE00 11.42
If I increase the number of k-means iterations to 10,000 (from a modest 10) (see options N and N' in the figure above), then we get a set where minimum `\Delta E` varies much less. We still have the same average `\textrm{avg} \Delta E = 9.1`.
> more colors.22.txt i 0 255 121 106 70 69 32 j 1 dE00 10.86 i 1 255 111 140 70 69 15 j 2 dE00 10.28 i 2 255 110 181 70 69 357 j 3 dE00 7.98 i 3 255 118 216 70 69 340 j 2 dE00 7.98 i 4 235 132 247 70 69 324 j 3 dE00 8.37 i 5 195 147 255 70 69 308 j 4 dE00 10.07 i 6 151 159 255 70 69 296 j 7 dE00 9.60 i 7 99 168 255 70 69 285 j 8 dE00 5.53 i 8 43 173 255 70 69 278 j 7 dE00 5.53 i 9 0 181 255 70 69 266 j 8 dE00 8.43 i 10 0 190 255 70 69 249 j 9 dE00 9.47 i 11 0 199 253 70 69 222 j 12 dE00 7.87 i 12 0 201 225 70 69 206 j 11 dE00 7.87 i 13 0 201 192 70 69 191 j 12 dE00 9.32 i 14 0 200 154 70 69 173 j 13 dE00 10.41 i 15 14 196 106 70 69 150 j 16 dE00 8.17 i 16 101 191 74 70 69 134 j 15 dE00 8.17 i 17 157 182 38 70 69 112 j 18 dE00 11.78 i 18 193 172 21 70 69 95 j 19 dE00 10.42 i 19 219 161 29 70 69 80 j 18 dE00 10.42 i 20 242 150 47 70 69 66 j 19 dE00 10.59 i 21 255 137 71 70 69 52 j 20 dE00 10.84
If we're only clustering 102 colors, then 10,000 iterations is practical.
If only one component is varying, clustering isn't very efficient. A better way to select colors in this case would be to step along the component and select adjacent colors based on a fixed `\Delta E`.
cytogenetic bands
Cytogenetic bands are chromosome landmarks obtained by Giemsa staining.
For these colors, I sampled from the grey Brewer palette. Stalks are variable regions in the five acrocentric chromosomes that connect the small arm to the chromosome.


The bands were composited on top of chromosomes at 30% opacity.

The the bands and chromosomes were further muted on the cover with a faint white overlay and two gradients were added to provide visibility to text.

genes
The genes in the graphic are taken from the OMIM database, which tracks genes associated with Mendelian disorders.

In the 2021-08-20 version of the database, there were 17,638 entries. The genomic position of each entry was taken as the midpoint between start and end position and the number of entry in each 250 kb region was tallied.
There were 6,973 regions that had non-zero counts of OMIM entries. The exact count of regions with a given number of entries is below. For example, there were 24 regions with 10 entries.
omim all 6973 omim 1 3097 size 1.0083 omim 2 1607 size 1.49850609149058 omim 3 846 size 1.88934938415614 omim 4 515 size 2.22703610655001 omim 5 290 size 2.53000291563677 omim 6 178 size 2.80789602411182 omim 7 136 size 3.06653415956866 omim 8 84 size 3.30975619521437 omim 9 68 size 3.54025696262142 omim 10 24 size 3.76001664243838 omim 11 42 size 3.97054229000266 omim 12 32 size 4.17301328612888 omim 13 12 size 4.36837373638714 omim 14 8 size 4.55739374975462 omim 15 9 size 4.74071154475013 omim 16 7 size 4.91886325486207 omim 17 6 size 5.09230456765918 omim 18 2 size 5.26142678164251 omim 19 1 size 5.4265689495722 omim 21 1 size 5.74606211035883 omim 22 1 size 5.90090430238019 omim 23 2 size 6.05275922451503 omim 24 1 size 6.2018107994994 omim 25 1 size 6.34822448986466 omim 26 2 size 6.4921498104568 omim 27 1 size 6.63372241603022
The last value in the list above is the radius of the circle used to encode the number of events in a region. The Flannery compensation was used in this encoding $$ r = 1.0083 r_0 \left( c/c_\textrm{min} \right)^{0.5716} $$
where `r_0` is the minimum radius, `c` is the count and `c_\textrm{min}` is the minimum count.
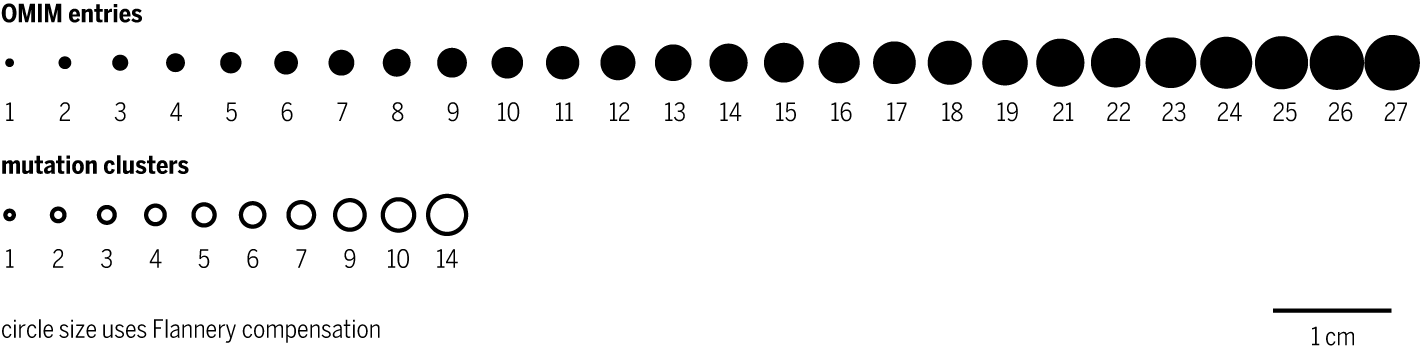
The same scheme was used for the mutation cluster circles.
mutation clusters
Mutation clusters were taken from Pan-cancer analysis of advanced patient tumors reveals interactions between therapy and genomic landscapes. (Pleasance E et al. (2020) Nature Cancer 1:452–468).

There were 2,596 clusters and their bin counts and circle sizes were as follows
cluster all 1823 cluster 1 1323 size 1.0083 cluster 2 343 size 1.49850609149058 cluster 3 96 size 1.88934938415614 cluster 4 38 size 2.22703610655001 cluster 5 10 size 2.53000291563677 cluster 6 6 size 2.80789602411182 cluster 7 4 size 3.06653415956866 cluster 9 1 size 3.54025696262142 cluster 10 1 size 3.76001664243838 cluster 14 1 size 4.55739374975462
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
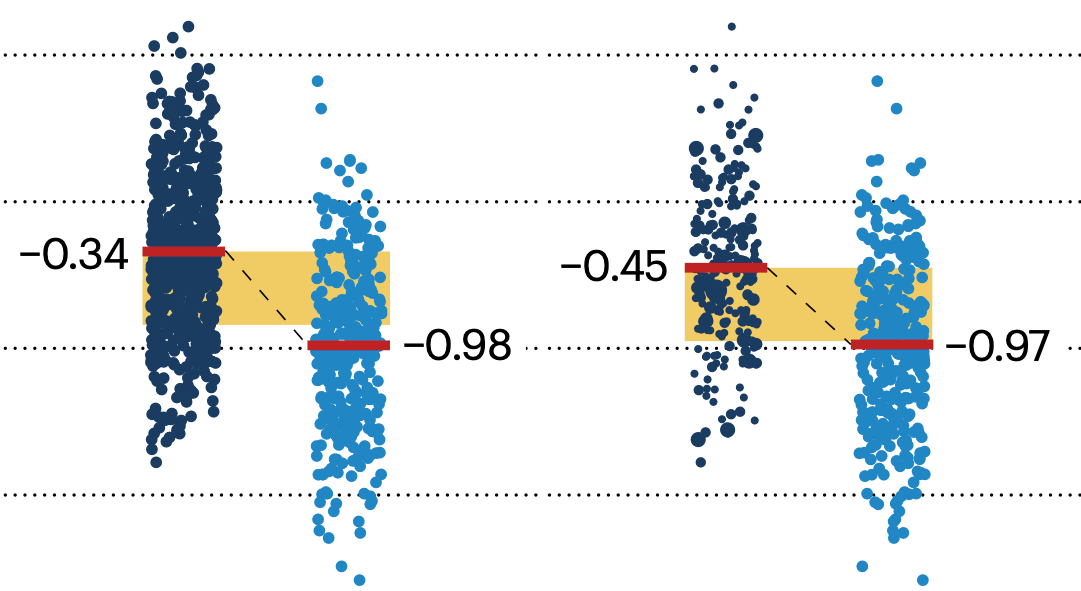
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
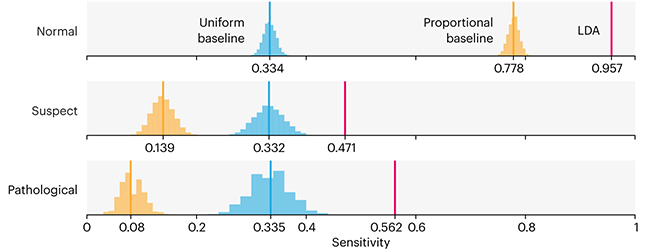
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 21:546–548.
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology