EMBO Journal 2011 Cover Contest
contents

For its 6 May 2009 issue, the EMBO Journal selected my submission of a large Circos figure for its cover. At the time, front page exposure of this sort has made Circos a very popular tool for visualization in genomics, and in particular, in cancer research where there is a need to illustrate differences between genomes.
Below I describe a couple of subsequent submissions for the EMBO Journal 2011 Cover Contest — a scientific entry and a non-scientific entry.
For the EMBO Journal 2011 Cover Contest, I prepared two entries, one for the scientific category and one for the non-scientific category.

The EMBO Journal non-scientific cover prize is awarded for the most interesting and beautiful image made outside the lab. Contestants may submit, for example, photos or artistic impressions of wildlife animals, plants or landscapes. Particularly welcome will also be hand or computer-generated paintings or drawings (or photographs of other works of art) related to a biological or molecular biological topic.
The EMBO Journal scientific cover prize is awarded for the most captivating and thought-provoking contribution depicting a piece of molecular biology research. Entries can include light or electron micrographs, 3D reconstructions or models of biological specimen or molecules, spectacular artefacts collected in the lab, original new views of lab equipment (but not of colleagues!), or other research-based images to be of interest to molecular biologists.


A large number of layout algorithms already exist to attempt to visualize networks. In an attempt to create attractive layouts, node and edge positions are optimized to minimize some fitness function, such as overlap or force (if edges are treated as springs). Unfortunately, as a result it is impossible to relate the position of a node (or the distance between any two nodes in the layout) to their connected neighbourhood in the network. This particularly holds for large networks, where nodes and edge overlap in the layout is unavoidable.
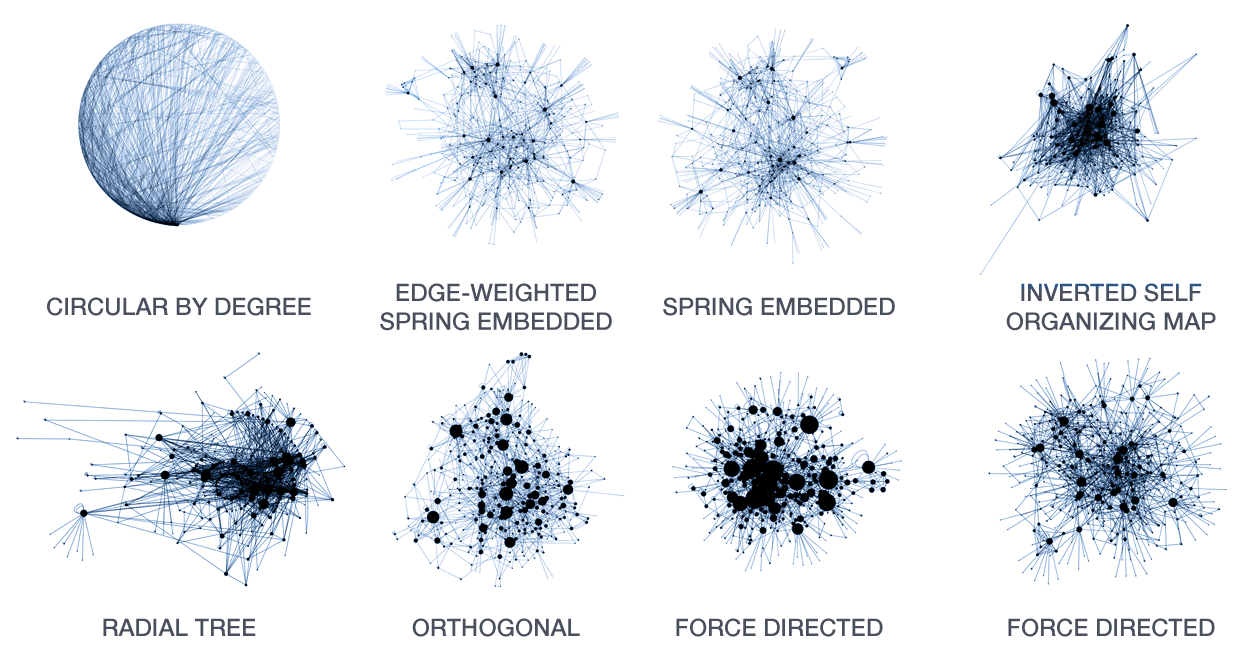
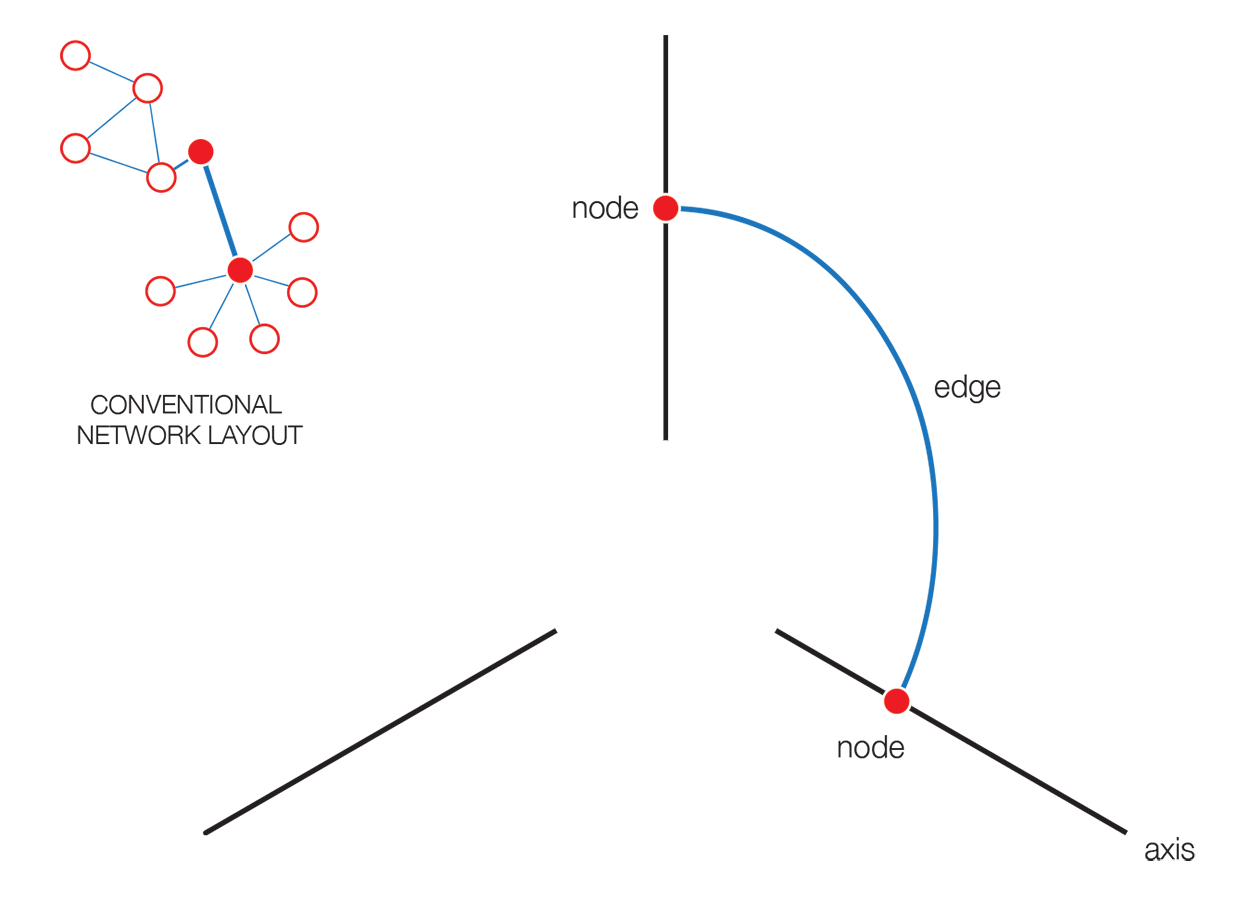
The hive plot is a rational approach to visualizing networks. It is designed to complement (at times, replace) the network hairball.
In a hive plot, network nodes are assigned to and placed on axes using rational rules. These rules typically are a function of local network structure around the node (connectivity, density, centrality, etc). The resulting plot is interpretable.
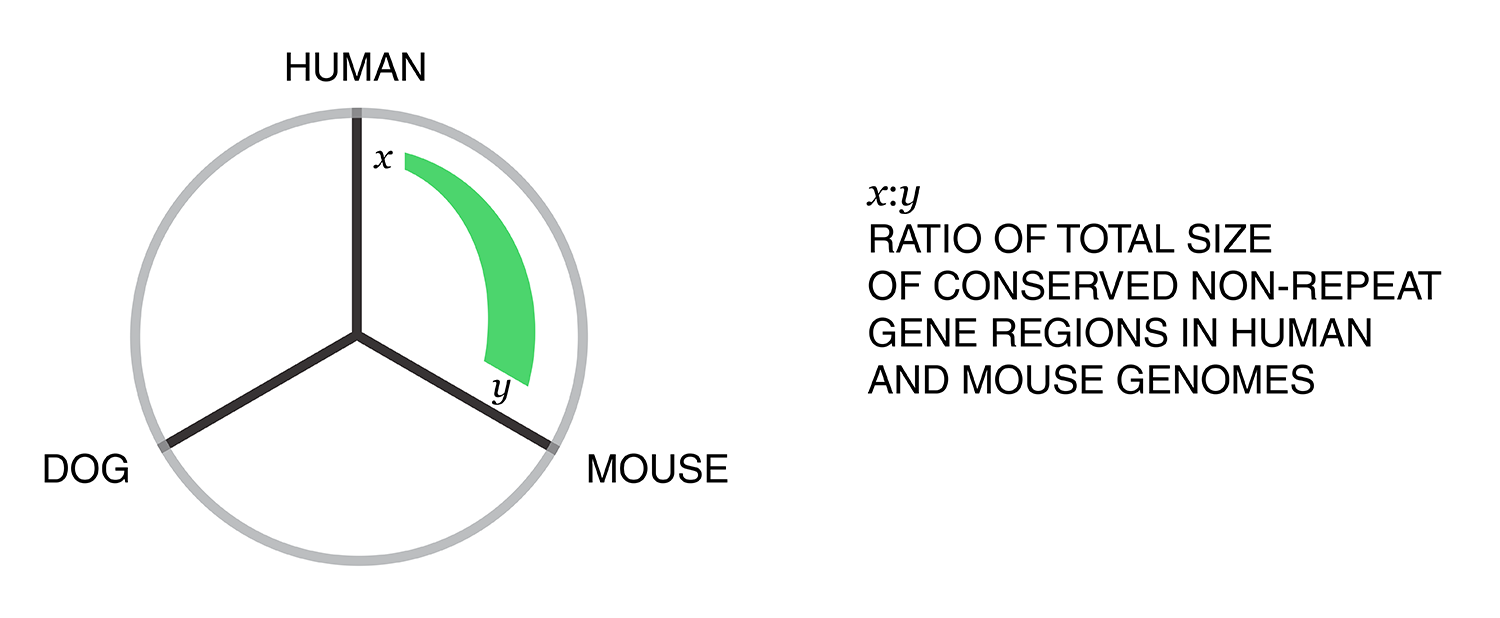
The hive plot can be applied to visualize a large number of ratios between three or more scales.
Instead of network edges, the lines in a hive plot now correspond to an (x,y) data pair, which can be interpreted as a ratio (x/y). This approach is particularly effective when lines are drawn as ribbons, which are then stacked. This is shown in the figure below.
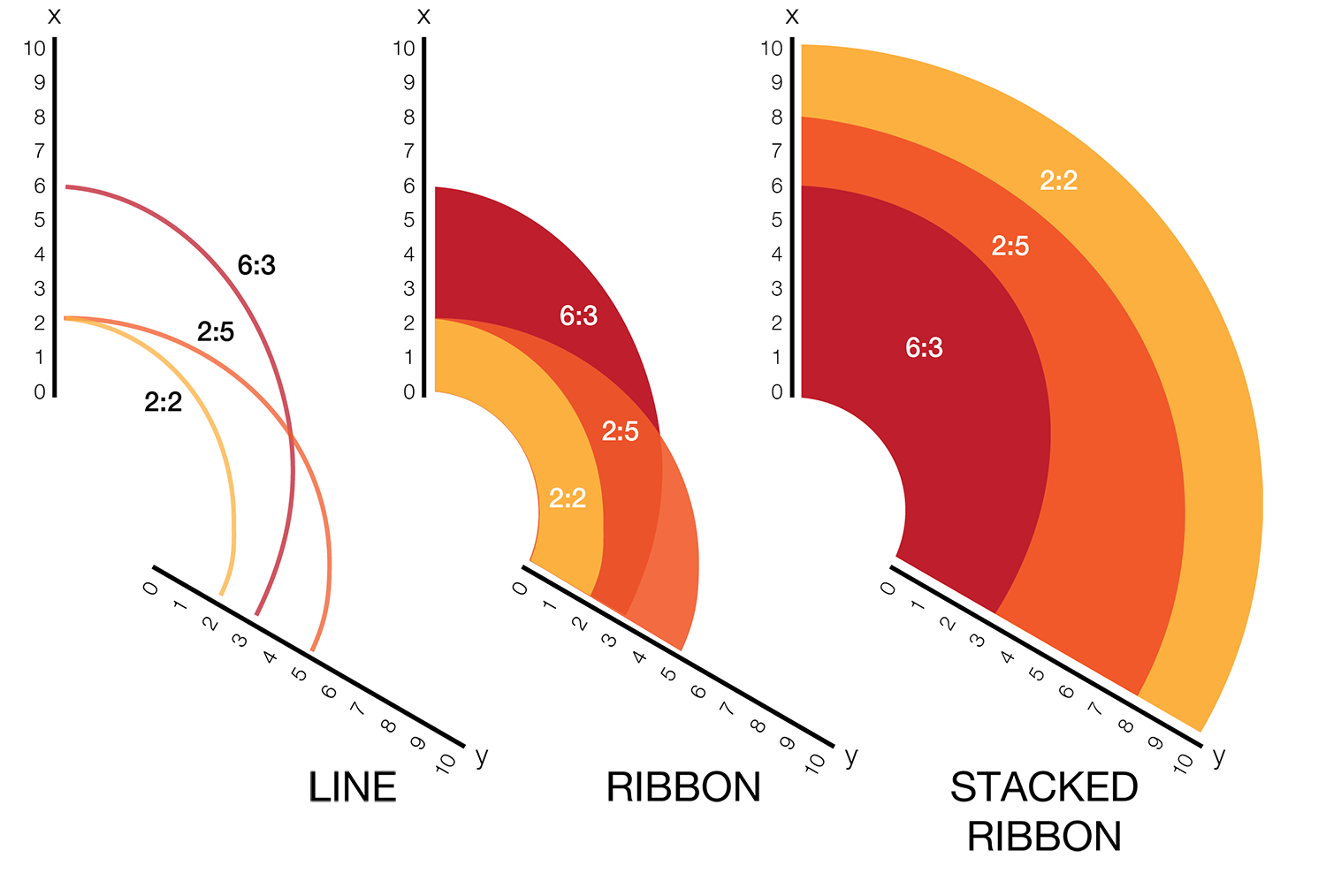
The resulting visualization bears resemblance to a stacked bar plot. The circular layout grants the advantage of being able to instantly compare all pair-wise comparisons between the axes (when three axes are used). This layout also gives the image a compare compact feel and is particularly suitable for tiling.
In the examples below, a 3-axis hive plot is shown with 8 ratios between each axis. The ratios are independent, in the sense that corresponding ribbons (e.g. blue) may have different thickness on either side of an axis. For example, if x:z = 2:3 and x:y = 1:3 then the ribbon on the left of the x axis will be twice as thick as on the right (see black arrow in figure below).
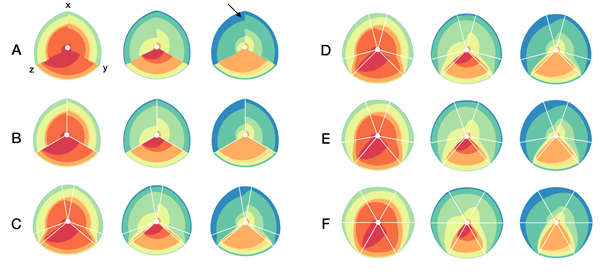
The axes in a hive plot can be arranged arbitrarily. In the figure above panels A and B show 24 ratios — 8 each between x/y, x/z, and y/x axes. In panels C-F each axis is split to create a single 6-axis plot from a dual 3-axis plot. The split axes reveal the transition between ribbons from the left and right sides.
The dual 3-axis plot appears more stylized and mathematical, whereas the single 6-axis plot is softer and organic. As the axis split distance is increased, the plots begin to look like surface density maps, which to some degree occludes the relationships between the ratio ribbons.
For each of human (hg18), mouse (mm8) and dog (canfam2) genome assemblies, UCSC annotations, available for each genome from the table browser, were used to hierarchically organize each base in the assembly using the following criteria: gene, repeat and gene+repeat. For each of these, bases were further categorized as conserved or not.
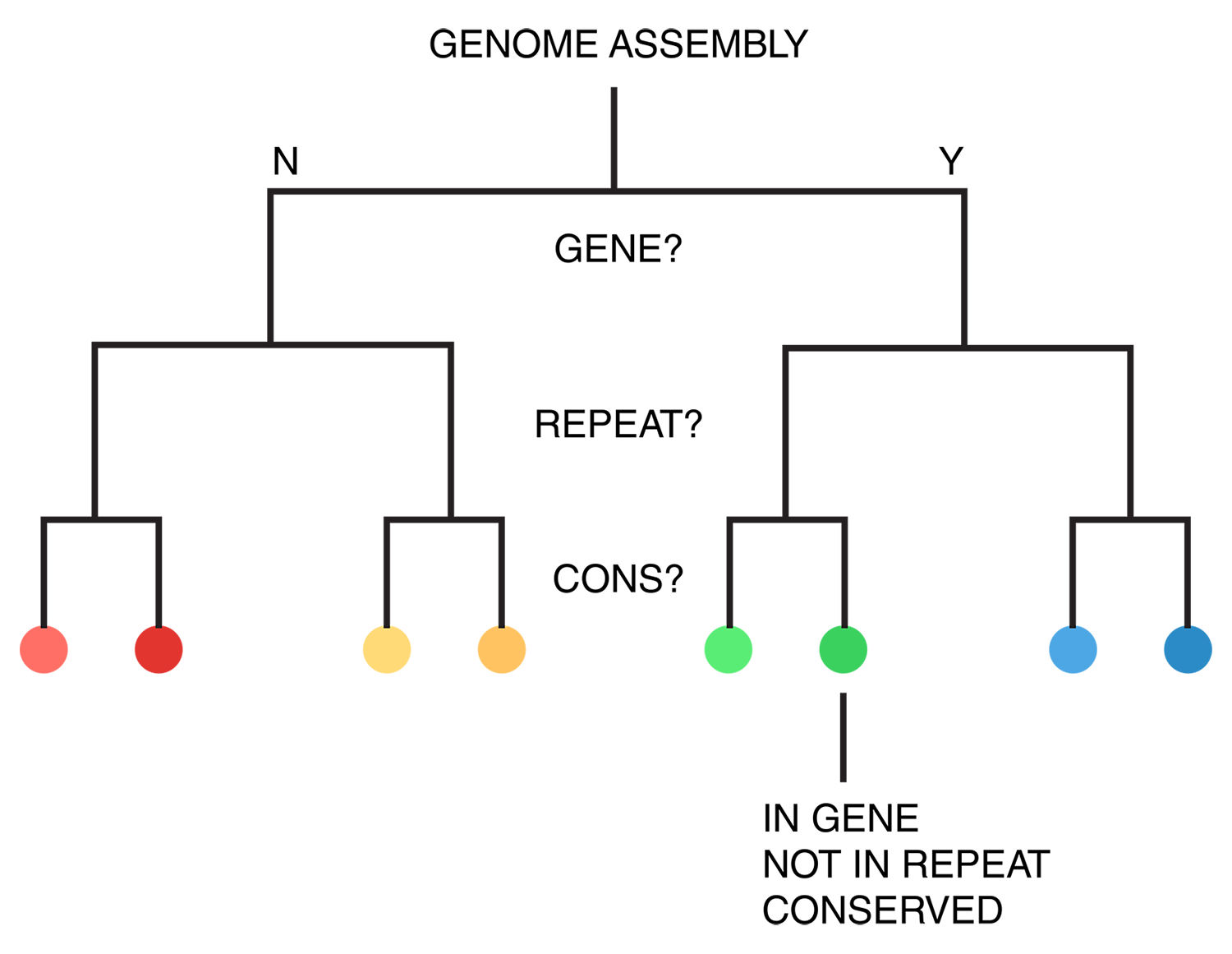
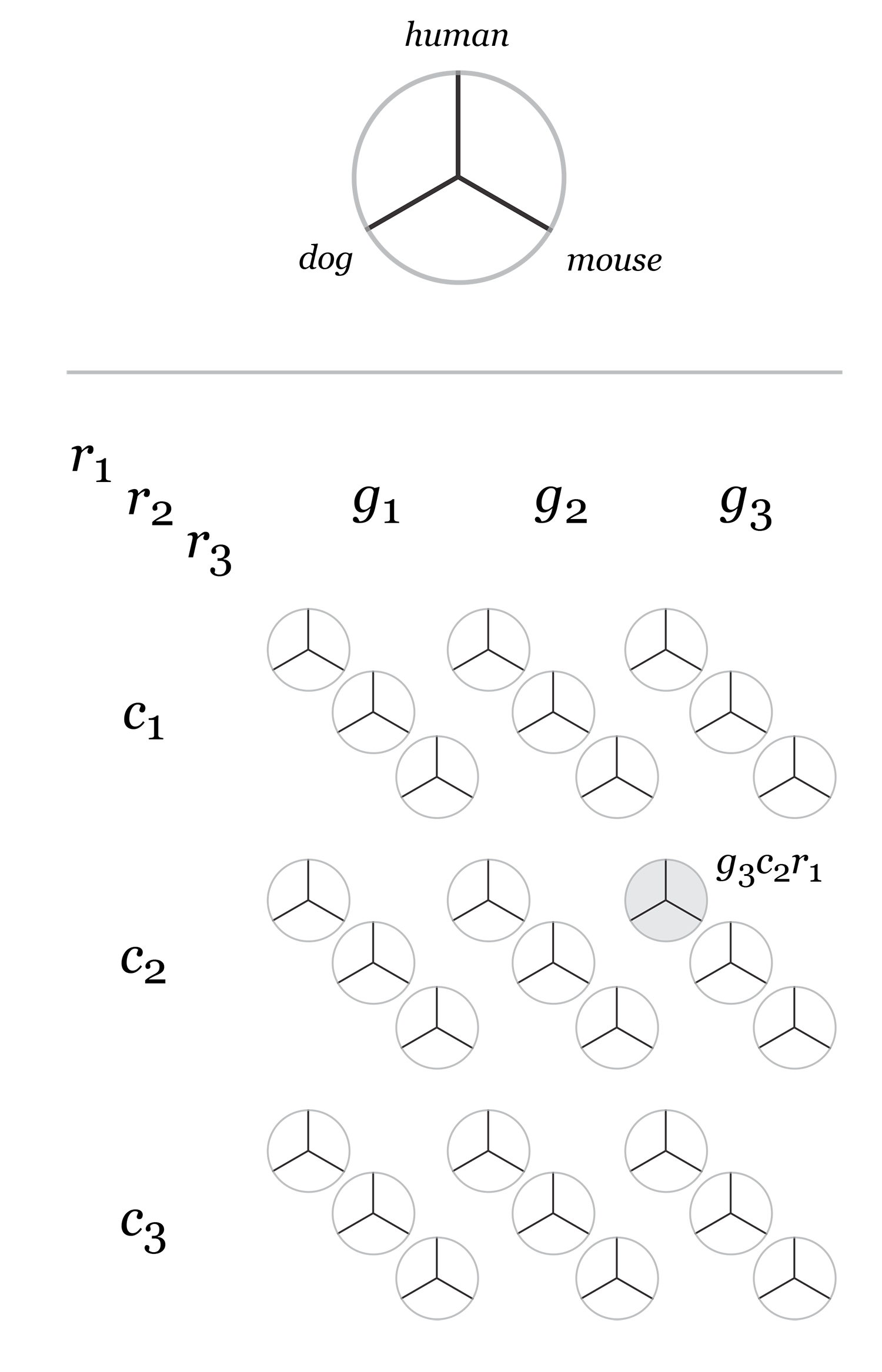
By exhaustively intersecting each of the annotation regions, the assembly was divided into disjoint segments, each with its annotation states. For example, below are a few adjacent regions from hg18 chr1 (a assembly, r repeat, c-cf conserved with dog, c-mm conserved with mouse).
... hg 1 120,942,663 120,945,658 2,996 a r hg 1 120,945,659 120,945,665 7 a hg 1 120,945,666 120,947,239 1,574 a c-cf c-mm hg 1 120,947,240 120,947,243 4 a c-cf c-mm r hg 1 120,947,244 120,947,268 25 a c-mm r hg 1 120,947,269 120,950,367 3,099 a r hg 1 120,950,368 120,950,386 19 a ...
Next, the total size of regions for each combination of annotation was calculated for each pairwise combination of genomes. The second genome in the pair dictates which conservation is used. For example, for the human-mouse pair, the relative fractions of the human genome that fall into each of the categories are
hg mm a 1,839,255,050 0.643542044483869 hg mm a,c-mm 757,027,260 0.264878365091574 hg mm a,r 206,719,589 0.0723296896425132 hg mm a,c-mm,r 42,358,464 0.0148209203088807 hg mm a,g 8,139,587 0.00284798264342638 hg mm a,c-mm,g 4,435,658 0.0015520046651231 hg mm a,g,r 48,994 1.71426463814481e-05 hg mm a,c-mm,g,r 33,869 1.18505182327074e-05
thus categorizing all the 2.86 Gb of the assembled human genome. The corresponding ratios for the mouse genome are
mm hg a 1,388,193,028 0.544355712823795 mm hg a,c-hg 892,892,218 0.350132128602082 mm hg a,r 196,173,508 0.0769260237089193 mm hg a,c-hg,r 62,305,053 0.0244318411447455 mm hg a,g 6,377,904 0.00250098394691097 mm hg a,c-hg,g 4,076,727 0.00159861747416369 mm hg a,g,r 81,889 3.21113447973805e-05 mm hg a,c-hg,g,r 57,585 2.2580954586784e-05
Using these two lists, all the ratios between the human and mouse axes can be determined. For example, for the conserved/gene/non-repeat regions the ratio of human:mouse is 0.00155:0.00160 (lines are bolded above). The corresponding ribbon for this ratio is shown below.
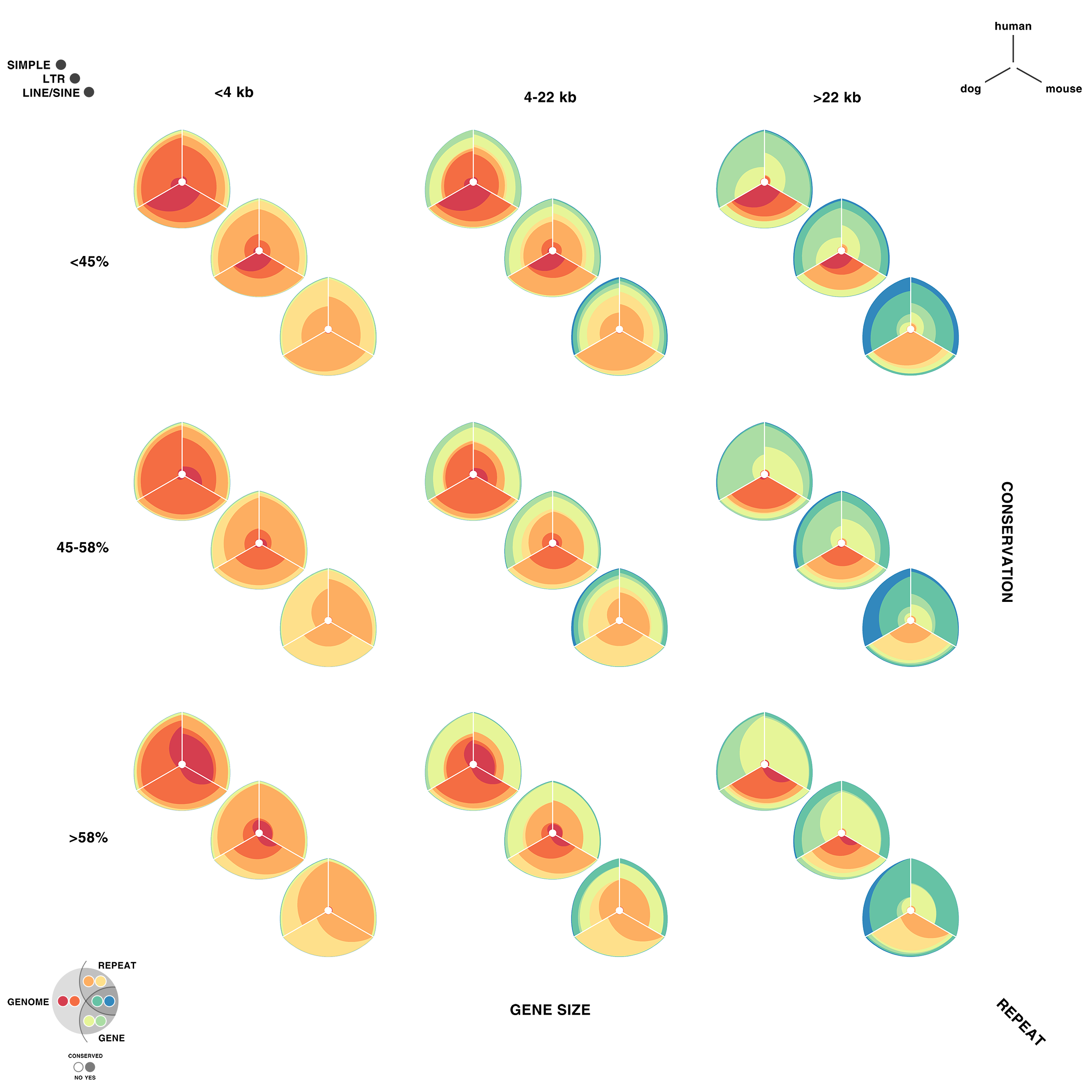
Category assignment into repeat, gene and conserved region was parametrized into three ranges for each criteria. These values were selected heuristically, to obtain a reasonable sample for each combination.
- gene g1 <4kb, g2 4kb-22kb, g3 >22kb
- repeat r1 simple, r2 LTR, r3 LINE/SINE
- conservation c1 <45%, c2 45%-58%, c3 >58%
Given 3 parameters for each of the categories, the full comparison is represented by 27 hive plots. These plots are arranged on the cover as follows
The scale of the axes was logarithmic to maintain visibility of all categories.
My 2011 non-scientific fiber optic entry received an honorouable mention. Oh well, we can't always have nice things.
Some time ago, I photographed fiber optic strands. These worked out well. I had not done anything with these images, and thought they would make a competitive entry into the cover contest.

I revisited the fiber optic lamp with a higher resolution camera (Canon 5D — original images were from a Canon 20D) and a dedicated macro lens (Sigma 150mm f2.8 EX APO DG HSM Macro) (original images were shot with the Canon EF 24-70L).
From these new images, shown below, I created five EMBO Journal cover submissions.

The submissions would render on the cover as shown below.





Beyond Belief Campaign BRCA Art
Fuelled by philanthropy, findings into the workings of BRCA1 and BRCA2 genes have led to groundbreaking research and lifesaving innovations to care for families facing cancer.
This set of 100 one-of-a-kind prints explore the structure of these genes. Each artwork is unique — if you put them all together, you get the full sequence of the BRCA1 and BRCA2 proteins.
Propensity score weighting
The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)
This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.
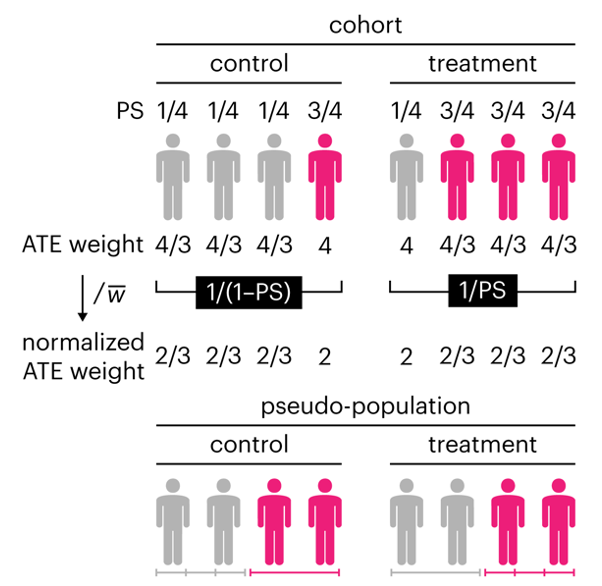
Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.
Happy 2025 π Day—
TTCAGT: a sequence of digits
Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.
Crafting 10 Years of Statistics Explanations: Points of Significance
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.
Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.
In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
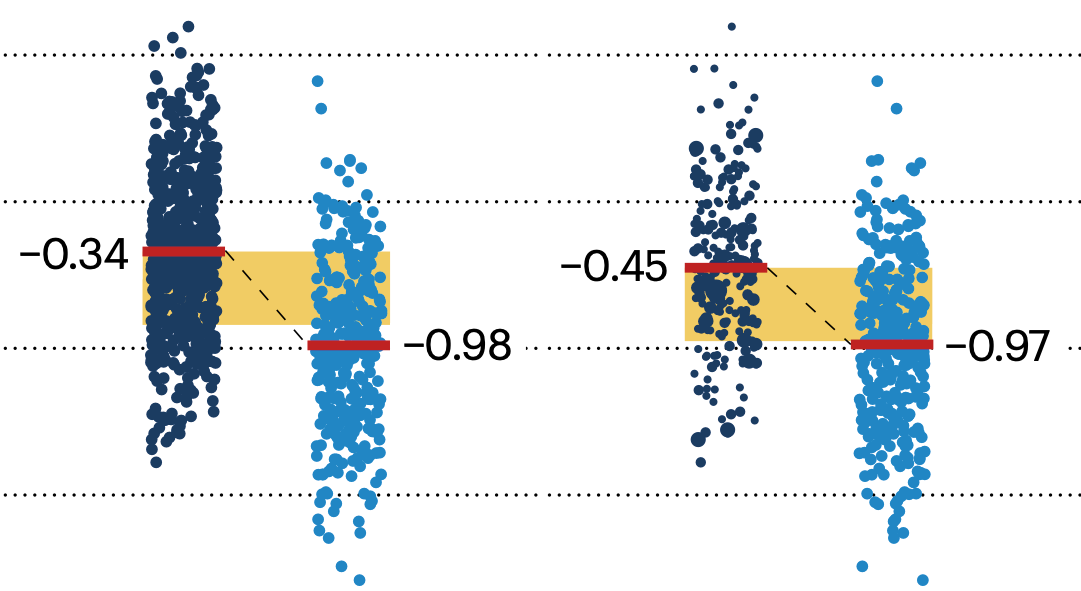
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Understanding p-values and significance
P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.
We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.



