fitness + math
`k` index: a crossfit and weightlifting benchmark
I want to diverge from my traditional scope of topics and propose a new benchmark for weightlifting and CrossFit: the `k` index.
The `k` index is brainy and fun and gives you a new way to structure your goals. At high values, it's very hard to increase, making each increment a huge challenge.
Going around with a t-shirt that says "`k=40` at everything" is maximally geeky and athletic.
definition of `k` index
For a given movement (e.g. squat, deadlift, press), you achieve index rank `k` if you can perform `k` unbroken reps at `k`% of your current one rep max (1RM).
Unbroken means no more than 1–2 seconds of pause between each rep. Exact standards would need to be established for competition.
example of `k` index
Suppose an athlete's one rep max (1RM) squat is 100 kg (220 lb).
The athlete will have a `k` index rating of `k=10` for squats if they can perform 10 unbroken reps at 10% 1RM, which is 10 kg (22 lb).
The athlete will have a `k` index rating of `k=20` for squats if they can perform 20 unbroken reps at 20% 1RM, which is 20 kg (44 lb).
The athlete will have an independent `k` index rating for other movements like deadlift and press. These ratings are likely to be different for each movement.
range of values
The minimum `k` index is `k=0` and it's a value we're born with.
The maximum theoretical `k` index is trivially `k=100` because, by definition, you cannot lift more than your current 1RM.
The maximum practical `k` index is much lower than `k=100` and probably in the range of `k = 50`.
expected `k` value
If you perform `r` reps at weight `w` you can estimate your 1RM using the Epley formula `w(1+r/30)` assuming `r>1`. In other words, for each rep at a weight `w` your estimate of your 1RM increases by ~3.3% above `w`.
There are various 1RM estimate equations and generally they are designed for fewer than 20 reps.
In some estimates, like by Mayhew et al. and by Wathan, the rep counts appear as `e^{-xr}` for small `x` such as `x=0.055` which makes the formula converge to a value when `r` is large like `r>15`. For example, Mayhew et al. converges to to a maximum of 1.91× of the weight being tested and Wathan converges to 2.05× of the weight being tested.
Other estimates, like McGlothin, generate unreasonable values for high rep count (e.g. 185 lb at 25 reps suggests a 1RM of 535 lb, which is insanely high) and for `r>37` gives negative estimates.
Therefore, while I'm reluctant to apply any of these equations to get a rough idea of an expected `k` value, I'm going to go ahead any way and use the Epley formula.
But let's try it anyway. If you lift `k` reps at `k`% 1RM and we assume Epley applies, $$ k/100 * 1RM * (1+k/30) = 1RM $$
which gives `k` to the nearest rep $$ k = 41 $$
Again, if Epley applies (which it probably doesn't), this means that if your `k > 41` you have more endurance relative to your level of strength.
Similarly, if your `k < 41` then your strength is higher relative to your level of endurance.
In the table below I provide the 1RM estimate for each `k` index value, which should give you an idea of how difficult it is to increase the `k` index.
From personal experience—I haven't tried this yet—achieving `k=30` is going to be hard and `k=40` feels to me like it would be extremely challenging.
testing `k` index
The `k` index requires more preparation and thought than testing your 1RM.
To accurately assess your `k` index you need to first have an accurate assessment of your 1RM. Thus, a proper 1RM test is a prerequisite.
Second, you need to pick a value of `k` to attempt to achieve and then attempt to perform the `k` reps at the required weight. If this is your first `k` index test, you need to pick `k` conservatively.
I suggest trying for `k=20` (20 reps at 20% 1RM). This should be doable for most people. Depending on how the 20th rep felt, you might want to take a 5 min rest and then try for `k=25` (25 reps at 25% 1RM). This should be exponentially harder than testing for `k=20`.
Everytime you retest your 1RM you need to retest your `k` index.
`k` index as a benchmark
The `k` index is a measure of muscle endurance and movement efficiency.
It is not a measure of raw strength, since it is not strictly a function of your 1RM—an athelete with a lower 1RM may have a higher `k` index for that movement.
It attempts to simplify multi-rep benchmarks like 3RM, 5RM, 10RM and so on. Although these themselves are very useful and I would not advocate forgetting about them, the `k` index adds a measure of grit into the mix.
As a single number, the `k` index can be used to visualize performance, especially in combination with 1RM. A plot of `k` vs 1RM would very nicely distinguish different training regimes, such as powerlifting (low `k` high 1RM) and CrossFit (high `k` lower 1RM).
Your `k` index may change independently of your 1RM, or vice versa. For example, you can get stronger and increase your 1RM but now find that your `k` index is lower.
I think most people can get `k=20`, or close to it, on their first try. The range between `k=30` and `k=50` is where things get interesting and very painful.
`h` index
The `k` index is similar to the h index, a metric commonly used in academic publishing.
The h index is defined as follows. "A scholar with an index of `h` has published `h` papers each of which has been cited in other papers at least `h` times.". For example, if I have an `h=10` then I have 10 papers that have at least 10 citations each.
To increase my `h` index to 11, it is not enough to publish a paper with 11 citations. Now, the other 10 papers also have to have an extra citation each.
`k` total WOD
In 1 hour, establish your `k` index for squats, deadlift and strict press, in that order. The total of your `k` index values is your `k` total.
Beginner athletes: attempt `k=20`, `k=24` and `k=27`.
Intermediate athletes: attempt `k=24`, `k=27` and `k=30`.
Elite athletes: attempt `k=30`, `k=32` and `k=34`.
The goal of this workout is to test all three `k` indexes in one session. You can test the individual movements on separate days and compare.
scope of use
The `k` index is only applicable for movements in which an athelete moves weight and for which a 1RM can be measured.
It does not apply to body weight movements like unweighted pushups or pullups. It can, however, apply to weighted forms of those movements.
Achieving the same `k` index for different movements may not be equally easy. For example, it's probably easier to have a `k=30` for deadlift than for strict press, since the latter uses smaller muscles.
usage and notation
All of the following are equivalent.
squat `k30`
`k30` (squat)
squat `k=30`
A squat `k` index of 30.
rep scheme table for `k` index
The table below shows the requirement for achieving each index assuming a 1RM of 100 kg.
The performance column gives the 1RM estimate using the Epley formula based on your rep count relative to the actual 1RM used to calculate the weight. For example, for `k=30` your 1RM estimate is `30/100 * (1+30/30) = 0.6` of your 1RM, which is lower than you estimated and you can said to be underperforming. On the other hand, if you manage `k=50` then your 1RM estimate based on your rep scheme is 1.33× the value used to calculate the weight.
As I mentioned above, the use of the Epley formula here is almost definitely wrong. However, I haven't done enough research in this field to know what formula to use for accurate 1RM estimation from a very high rep count. It's possible that no such accurate assessment can be made and I need to try to at least try it for myself in the gym.
| k | reps | performance |
|---|---|---|
| 1 | 1 @ 1% 1RM (1 kg) | 0.01 |
| 2 | 2 @ 2% 1RM (2 kg) | 0.02 |
| 3 | 3 @ 3% 1RM (3 kg) | 0.03 |
| 4 | 4 @ 4% 1RM (4 kg) | 0.05 |
| 5 | 5 @ 5% 1RM (5 kg) | 0.06 |
| 6 | 6 @ 6% 1RM (6 kg) | 0.07 |
| 7 | 7 @ 7% 1RM (7 kg) | 0.09 |
| 8 | 8 @ 8% 1RM (8 kg) | 0.10 |
| 9 | 9 @ 9% 1RM (9 kg) | 0.12 |
| 10 | 10 @ 10% 1RM (10 kg) | 0.13 |
| 11 | 11 @ 11% 1RM (11 kg) | 0.15 |
| 12 | 12 @ 12% 1RM (12 kg) | 0.17 |
| 13 | 13 @ 13% 1RM (13 kg) | 0.19 |
| 14 | 14 @ 14% 1RM (14 kg) | 0.21 |
| 15 | 15 @ 15% 1RM (15 kg) | 0.22 |
| 16 | 16 @ 16% 1RM (16 kg) | 0.25 |
| 17 | 17 @ 17% 1RM (17 kg) | 0.27 |
| 18 | 18 @ 18% 1RM (18 kg) | 0.29 |
| 19 | 19 @ 19% 1RM (19 kg) | 0.31 |
| 20 | 20 @ 20% 1RM (20 kg) | 0.33 |
| 21 | 21 @ 21% 1RM (21 kg) | 0.36 |
| 22 | 22 @ 22% 1RM (22 kg) | 0.38 |
| 23 | 23 @ 23% 1RM (23 kg) | 0.41 |
| 24 | 24 @ 24% 1RM (24 kg) | 0.43 |
| 25 | 25 @ 25% 1RM (25 kg) | 0.46 |
| 26 | 26 @ 26% 1RM (26 kg) | 0.49 |
| 27 | 27 @ 27% 1RM (27 kg) | 0.51 |
| 28 | 28 @ 28% 1RM (28 kg) | 0.54 |
| 29 | 29 @ 29% 1RM (29 kg) | 0.57 |
| 30 | 30 @ 30% 1RM (30 kg) | 0.60 |
| 31 | 31 @ 31% 1RM (31 kg) | 0.63 |
| 32 | 32 @ 32% 1RM (32 kg) | 0.66 |
| 33 | 33 @ 33% 1RM (33 kg) | 0.69 |
| 34 | 34 @ 34% 1RM (34 kg) | 0.73 |
| 35 | 35 @ 35% 1RM (35 kg) | 0.76 |
| 36 | 36 @ 36% 1RM (36 kg) | 0.79 |
| 37 | 37 @ 37% 1RM (37 kg) | 0.83 |
| 38 | 38 @ 38% 1RM (38 kg) | 0.86 |
| 39 | 39 @ 39% 1RM (39 kg) | 0.90 |
| 40 | 40 @ 40% 1RM (40 kg) | 0.93 |
| 41 | 41 @ 41% 1RM (41 kg) | 0.97 |
| 42 | 42 @ 42% 1RM (42 kg) | 1.01 |
| 43 | 43 @ 43% 1RM (43 kg) | 1.05 |
| 44 | 44 @ 44% 1RM (44 kg) | 1.09 |
| 45 | 45 @ 45% 1RM (45 kg) | 1.12 |
| 46 | 46 @ 46% 1RM (46 kg) | 1.17 |
| 47 | 47 @ 47% 1RM (47 kg) | 1.21 |
| 48 | 48 @ 48% 1RM (48 kg) | 1.25 |
| 49 | 49 @ 49% 1RM (49 kg) | 1.29 |
| 50 | 50 @ 50% 1RM (50 kg) | 1.33 |
| k | reps | performance |
|---|---|---|
| 51 | 51 @ 51% 1RM (51 kg) | 1.38 |
| 52 | 52 @ 52% 1RM (52 kg) | 1.42 |
| 53 | 53 @ 53% 1RM (53 kg) | 1.47 |
| 54 | 54 @ 54% 1RM (54 kg) | 1.51 |
| 55 | 55 @ 55% 1RM (55 kg) | 1.56 |
| 56 | 56 @ 56% 1RM (56 kg) | 1.61 |
| 57 | 57 @ 57% 1RM (57 kg) | 1.65 |
| 58 | 58 @ 58% 1RM (58 kg) | 1.70 |
| 59 | 59 @ 59% 1RM (59 kg) | 1.75 |
| 60 | 60 @ 60% 1RM (60 kg) | 1.80 |
| 61 | 61 @ 61% 1RM (61 kg) | 1.85 |
| 62 | 62 @ 62% 1RM (62 kg) | 1.90 |
| 63 | 63 @ 63% 1RM (63 kg) | 1.95 |
| 64 | 64 @ 64% 1RM (64 kg) | 2.01 |
| 65 | 65 @ 65% 1RM (65 kg) | 2.06 |
| 66 | 66 @ 66% 1RM (66 kg) | 2.11 |
| 67 | 67 @ 67% 1RM (67 kg) | 2.17 |
| 68 | 68 @ 68% 1RM (68 kg) | 2.22 |
| 69 | 69 @ 69% 1RM (69 kg) | 2.28 |
| 70 | 70 @ 70% 1RM (70 kg) | 2.33 |
| 71 | 71 @ 71% 1RM (71 kg) | 2.39 |
| 72 | 72 @ 72% 1RM (72 kg) | 2.45 |
| 73 | 73 @ 73% 1RM (73 kg) | 2.51 |
| 74 | 74 @ 74% 1RM (74 kg) | 2.57 |
| 75 | 75 @ 75% 1RM (75 kg) | 2.62 |
| 76 | 76 @ 76% 1RM (76 kg) | 2.69 |
| 77 | 77 @ 77% 1RM (77 kg) | 2.75 |
| 78 | 78 @ 78% 1RM (78 kg) | 2.81 |
| 79 | 79 @ 79% 1RM (79 kg) | 2.87 |
| 80 | 80 @ 80% 1RM (80 kg) | 2.93 |
| 81 | 81 @ 81% 1RM (81 kg) | 3.00 |
| 82 | 82 @ 82% 1RM (82 kg) | 3.06 |
| 83 | 83 @ 83% 1RM (83 kg) | 3.13 |
| 84 | 84 @ 84% 1RM (84 kg) | 3.19 |
| 85 | 85 @ 85% 1RM (85 kg) | 3.26 |
| 86 | 86 @ 86% 1RM (86 kg) | 3.33 |
| 87 | 87 @ 87% 1RM (87 kg) | 3.39 |
| 88 | 88 @ 88% 1RM (88 kg) | 3.46 |
| 89 | 89 @ 89% 1RM (89 kg) | 3.53 |
| 90 | 90 @ 90% 1RM (90 kg) | 3.60 |
| 91 | 91 @ 91% 1RM (91 kg) | 3.67 |
| 92 | 92 @ 92% 1RM (92 kg) | 3.74 |
| 93 | 93 @ 93% 1RM (93 kg) | 3.81 |
| 94 | 94 @ 94% 1RM (94 kg) | 3.89 |
| 95 | 95 @ 95% 1RM (95 kg) | 3.96 |
| 96 | 96 @ 96% 1RM (96 kg) | 4.03 |
| 97 | 97 @ 97% 1RM (97 kg) | 4.11 |
| 98 | 98 @ 98% 1RM (98 kg) | 4.18 |
| 99 | 99 @ 99% 1RM (99 kg) | 4.26 |
| 100 | 100 @ 100% 1RM (100 kg) | 4.33 |
Beyond Belief Campaign BRCA Art
Fuelled by philanthropy, findings into the workings of BRCA1 and BRCA2 genes have led to groundbreaking research and lifesaving innovations to care for families facing cancer.
This set of 100 one-of-a-kind prints explore the structure of these genes. Each artwork is unique — if you put them all together, you get the full sequence of the BRCA1 and BRCA2 proteins.
Propensity score weighting
The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)
This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.
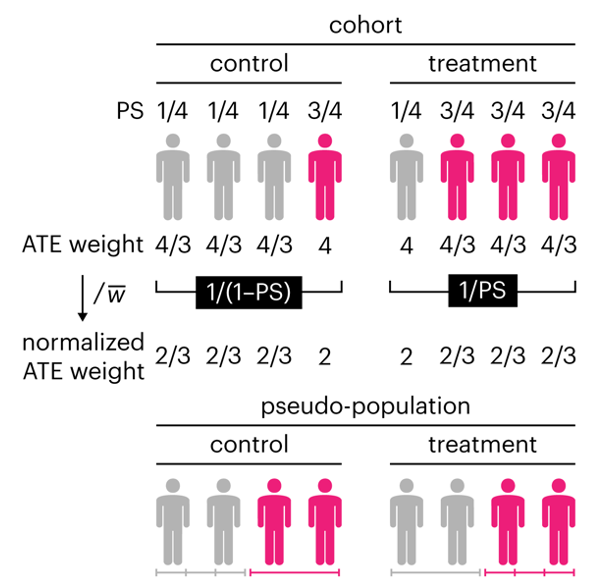
Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.
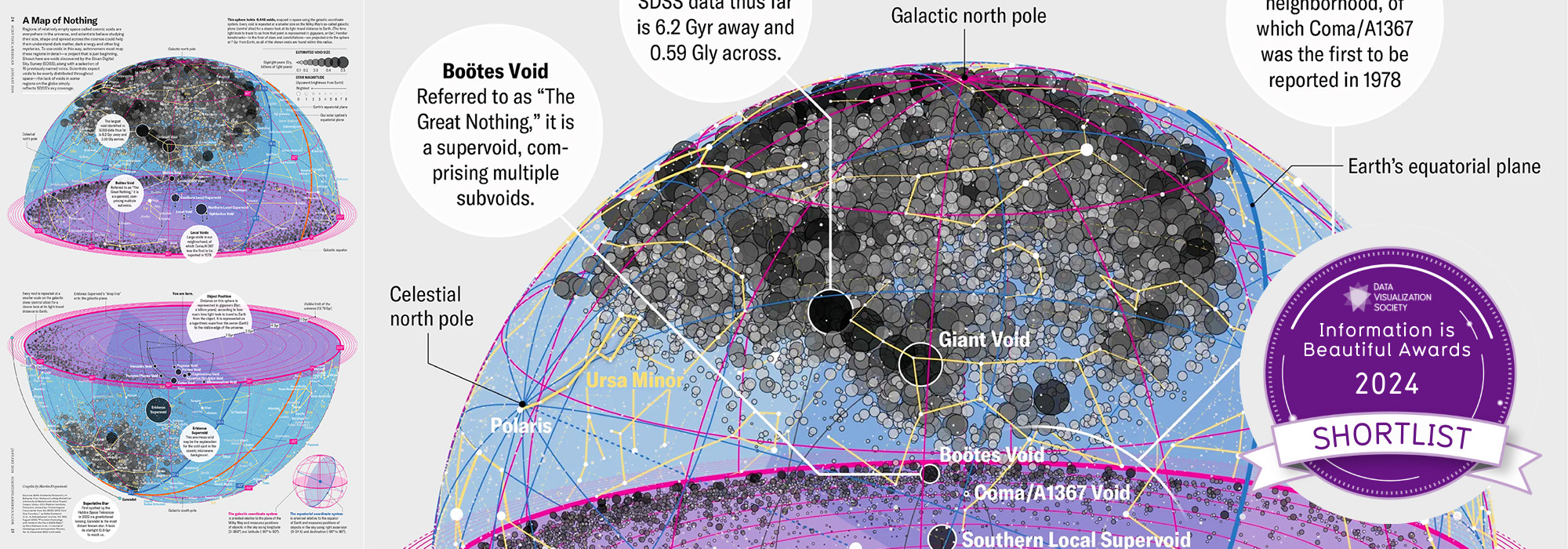
Happy 2025 π Day—
TTCAGT: a sequence of digits
Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.
Crafting 10 Years of Statistics Explanations: Points of Significance
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.
Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.
In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.
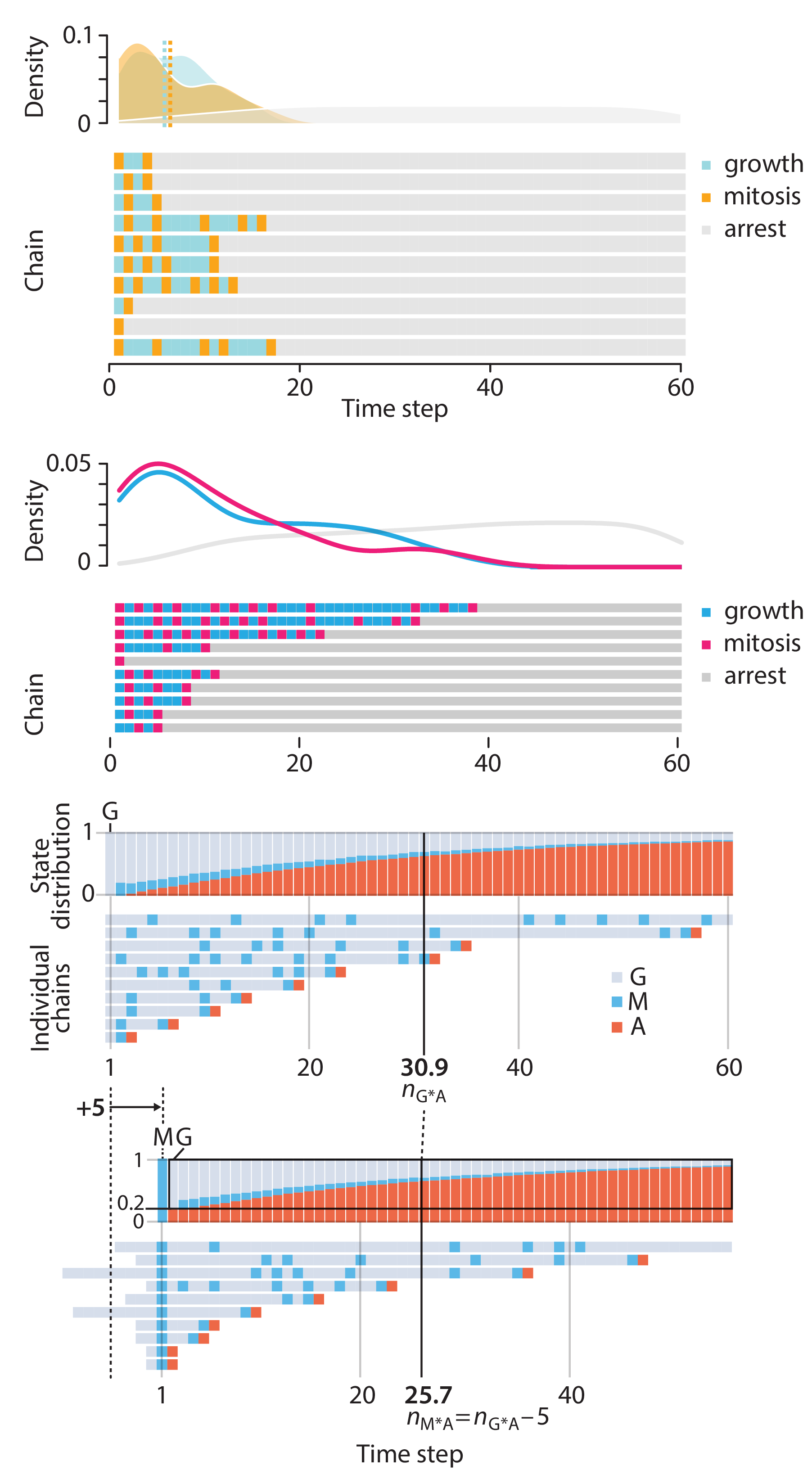
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.
Propensity score matching
I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player
In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.
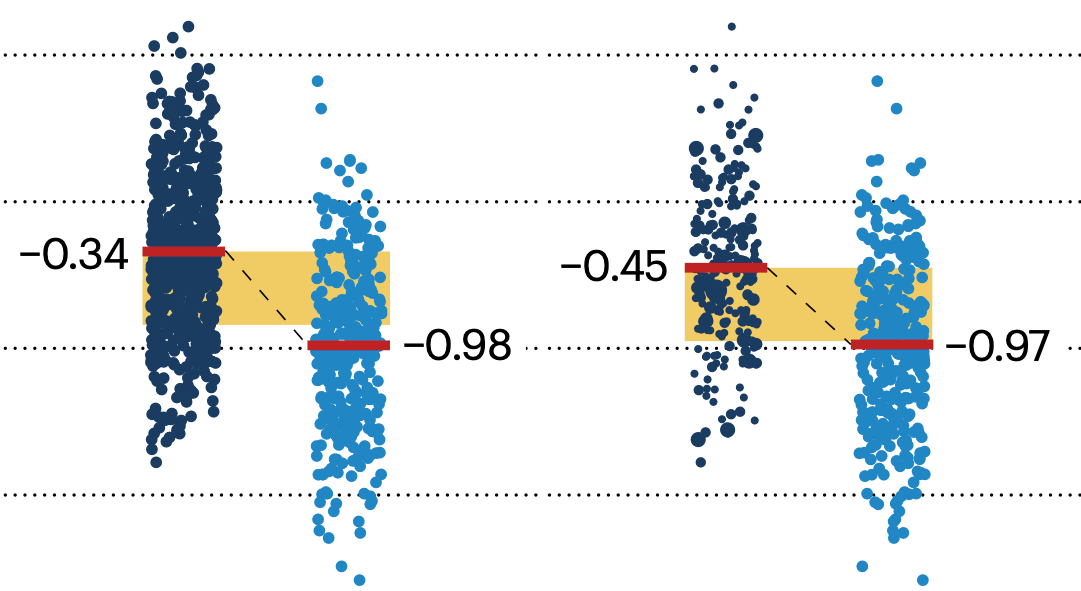
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.
Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.
Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.
Understanding p-values and significance
P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.
We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.
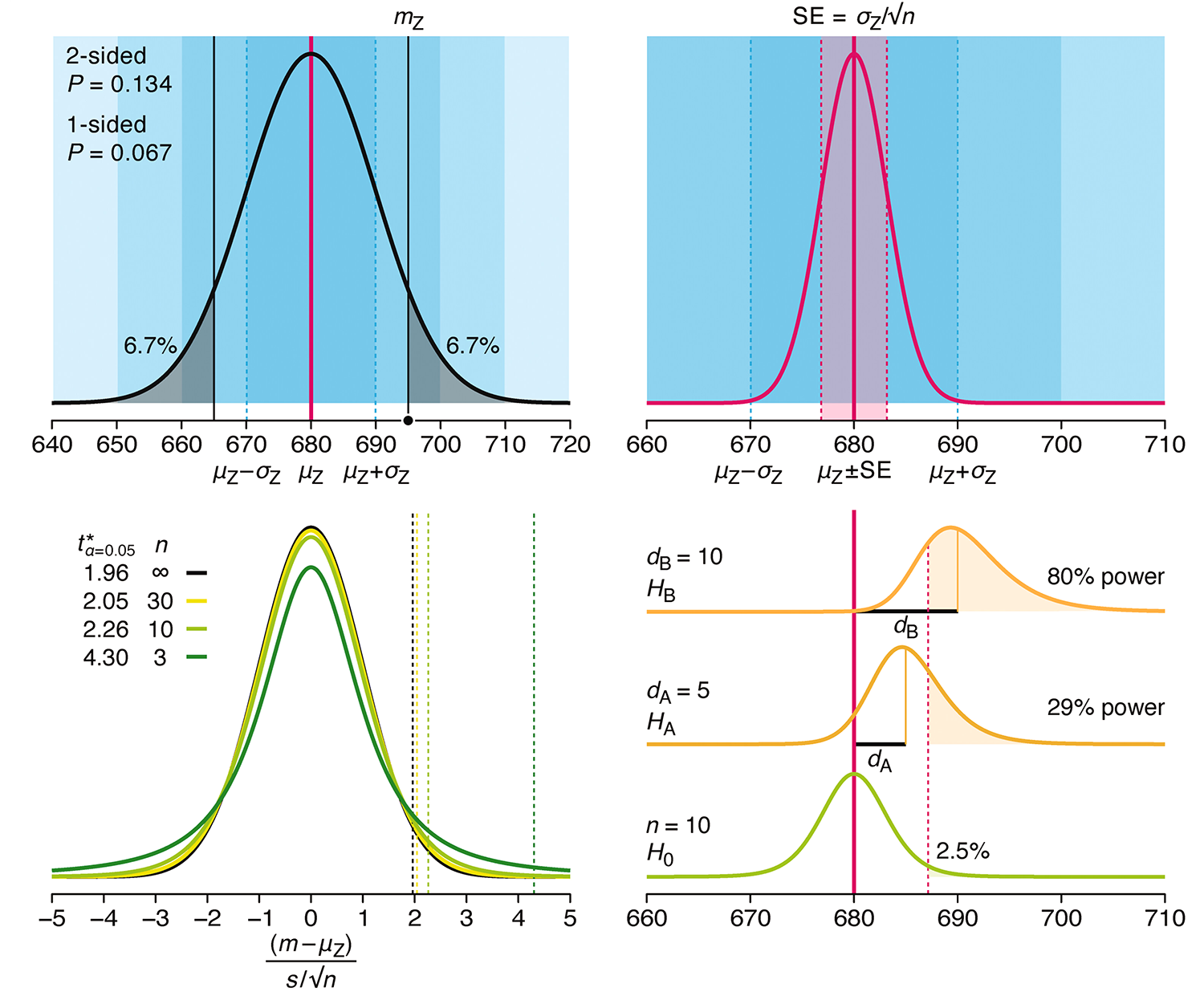
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.