visualization + design

Statistics for aneuploidy level `h` = 1 2 3 4 5 6 7 8 9 10

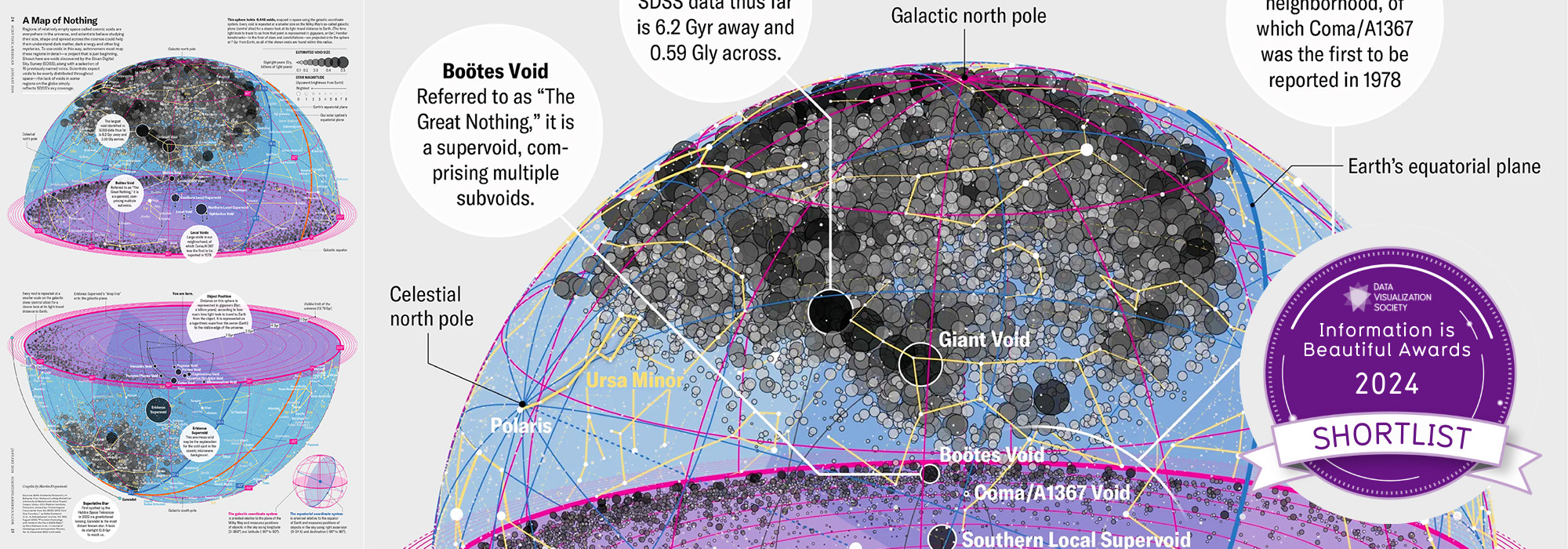
Haploid Genome Coverage Tables

Given a location `x` defined in the context of `h` chromosomes, the probability that position `x` is covered at least `\phi` times is `P_{h,\phi}` and given by $$ P_{h,\phi} = \left( 1 - \sum \frac{1}{k!} \left( \frac{\rho}{h}^k \right) e^{-\rho/h} \right)^h \tag{1} $$

For more details, see Wendl, M.C. and R.K. Wilson. 2008. Aspects of coverage in medical DNA sequencing. BMC Bioinformatics 9: 239.

For a given sequencing redundancy `\rho` (e.g. `\rho`-fold, as determined by the length of the haploid genome) of a haploid genome, the fraction of the haploid genome represented by at least `\phi` reads is reported by `P_{h,\phi}`. Coverage by fewer than `\phi` reads is reported as `1-P_{h,\phi}`. Coverage by exactly `\phi` reads is `P_{h,\phi} - P_{h,\phi+1}`. Entries for which fractional coverage is `\lt 10^{-5}` are not shown.

A rudimentary Monte Carlo simulation of genome coverage is also available, and is a useful supplement to the exact probabilities shown here.

CUSTOM DEPTH AND PLOIDY To create a table with a specific ploidy (e.g. 12) and haploid-equivalent (see below) depth (e.g. `200 \times`), use

http://mkweb.bcgsc.ca/coverage/?aneuploidy=12&depth=200

EXAMPLE 1

Suppose you carried out 3-fold redundant (`\rho=3`) sequencing of a haploid genome (`h=1`). 95.02% of the genome will be covered by at least one read (`P_{1,1}`) while 22.40% will be covered by exactly 3 reads (`P_{1,3} - P_{1,4}`).

EXAMPLE 2

You are sequencing a sample with a tumor content of 25% and you're interested in the depth of sequencing required to detect heterozygous mutations in the tumor. This scenario is equivalent to an aneuploidy = 8 genome—any given allele is present 8 times. If you sequence at (`\rho=200`), then 95% of the bases will be covered at a depth of at least `\phi = 14` (`P_{8,14} = 0.9494`). If you're satisfied with `\phi = 5` then you only need `\rho = 100` since now `P_{8,5} = 0.9580`.

ANALYTICAL vs STOCHASTIC

View plot that compares analytical vs stochastic results.

HAPLOID vs DIPLOID

View plot that compares 100x and 200x coverage of haploid and diploid genomes.

CODE

Download Perl scripts for analytical (to produce the tables below for any `\rho`) and stochastic coverage calculations.

sequencing redundancy for a haploid genome

View table for sequencing redundancy `\rho` = 1 2 3 4 5 6 7 8 9 10 20 25 50 75 100 of a haploid genome.

IMPORTANT The redundancy is always calculated using the size of the haploid genome. For example, if we collect 600 Gb of reads, our sequencing redundancy is `600 / 3 = 200 \times`. We've used the length of the haploid genome (3 Gb) in the calculation. If we now apply this `200 \times` sequencing to a diploid genome, our average coverage will not be `200 \times` but slightly less than `100 \times`.

sequencing redundancy 1-fold (`\rho / h = 1.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.3679	0.0000	1.0000
1	0.3679	0.3679	0.6321
2	0.1839	0.7358	0.2642
3	0.0613	0.9197	0.0803
4	0.0153	0.9810	0.0190
5	0.0031	0.9963	0.0037

sequencing redundancy 2-fold (`\rho / h = 2.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.1353	0.0000	1.0000
1	0.2707	0.1353	0.8647
2	0.2707	0.4060	0.5940
3	0.1804	0.6767	0.3233
4	0.0902	0.8571	0.1429
5	0.0361	0.9473	0.0527
6	0.0120	0.9834	0.0166
7	0.0034	0.9955	0.0045
8	0.0009	0.9989	0.0011
9	0.0002	0.9998	0.0002
10	0.0000	1.0000	0.0000

sequencing redundancy 3-fold (`\rho / h = 3.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0498	0.0000	1.0000
1	0.1494	0.0498	0.9502
2	0.2240	0.1991	0.8009
3	0.2240	0.4232	0.5768
4	0.1680	0.6472	0.3528
5	0.1008	0.8153	0.1847
6	0.0504	0.9161	0.0839
7	0.0216	0.9665	0.0335
8	0.0081	0.9881	0.0119
9	0.0027	0.9962	0.0038
10	0.0008	0.9989	0.0011
11	0.0002	0.9997	0.0003
12	0.0001	0.9999	0.0001
13	0.0000	1.0000	0.0000

sequencing redundancy 4-fold (`\rho / h = 4.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0183	0.0000	1.0000
1	0.0733	0.0183	0.9817
2	0.1465	0.0916	0.9084
3	0.1954	0.2381	0.7619
4	0.1954	0.4335	0.5665
5	0.1563	0.6288	0.3712
6	0.1042	0.7851	0.2149
7	0.0595	0.8893	0.1107
8	0.0298	0.9489	0.0511
9	0.0132	0.9786	0.0214
10	0.0053	0.9919	0.0081
11	0.0019	0.9972	0.0028
12	0.0006	0.9991	0.0009
13	0.0002	0.9997	0.0003
14	0.0001	0.9999	0.0001
15	0.0000	1.0000	0.0000

sequencing redundancy 5-fold (`\rho / h = 5.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0067	0.0000	1.0000
1	0.0337	0.0067	0.9933
2	0.0842	0.0404	0.9596
3	0.1404	0.1247	0.8753
4	0.1755	0.2650	0.7350
5	0.1755	0.4405	0.5595
6	0.1462	0.6160	0.3840
7	0.1044	0.7622	0.2378
8	0.0653	0.8666	0.1334
9	0.0363	0.9319	0.0681
10	0.0181	0.9682	0.0318
11	0.0082	0.9863	0.0137
12	0.0034	0.9945	0.0055
13	0.0013	0.9980	0.0020
14	0.0005	0.9993	0.0007
15	0.0002	0.9998	0.0002
16	0.0000	0.9999	0.0001
17	0.0000	1.0000	0.0000

sequencing redundancy 6-fold (`\rho / h = 6.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0025	0.0000	1.0000
1	0.0149	0.0025	0.9975
2	0.0446	0.0174	0.9826
3	0.0892	0.0620	0.9380
4	0.1339	0.1512	0.8488
5	0.1606	0.2851	0.7149
6	0.1606	0.4457	0.5543
7	0.1377	0.6063	0.3937
8	0.1033	0.7440	0.2560
9	0.0688	0.8472	0.1528
10	0.0413	0.9161	0.0839
11	0.0225	0.9574	0.0426
12	0.0113	0.9799	0.0201
13	0.0052	0.9912	0.0088
14	0.0022	0.9964	0.0036
15	0.0009	0.9986	0.0014
16	0.0003	0.9995	0.0005
17	0.0001	0.9998	0.0002
18	0.0000	0.9999	0.0001
19	0.0000	1.0000	0.0000

sequencing redundancy 7-fold (`\rho / h = 7.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0009	0.0000	1.0000
1	0.0064	0.0009	0.9991
2	0.0223	0.0073	0.9927
3	0.0521	0.0296	0.9704
4	0.0912	0.0818	0.9182
5	0.1277	0.1730	0.8270
6	0.1490	0.3007	0.6993
7	0.1490	0.4497	0.5503
8	0.1304	0.5987	0.4013
9	0.1014	0.7291	0.2709
10	0.0710	0.8305	0.1695
11	0.0452	0.9015	0.0985
12	0.0263	0.9467	0.0533
13	0.0142	0.9730	0.0270
14	0.0071	0.9872	0.0128
15	0.0033	0.9943	0.0057
16	0.0014	0.9976	0.0024
17	0.0006	0.9990	0.0010
18	0.0002	0.9996	0.0004
19	0.0001	0.9999	0.0001
20	0.0000	1.0000	0.0000
21	0.0000	1.0000	0.0000

sequencing redundancy 8-fold (`\rho / h = 8.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0003	0.0000	1.0000
1	0.0027	0.0003	0.9997
2	0.0107	0.0030	0.9970
3	0.0286	0.0138	0.9862
4	0.0573	0.0424	0.9576
5	0.0916	0.0996	0.9004
6	0.1221	0.1912	0.8088
7	0.1396	0.3134	0.6866
8	0.1396	0.4530	0.5470
9	0.1241	0.5925	0.4075
10	0.0993	0.7166	0.2834
11	0.0722	0.8159	0.1841
12	0.0481	0.8881	0.1119
13	0.0296	0.9362	0.0638
14	0.0169	0.9658	0.0342
15	0.0090	0.9827	0.0173
16	0.0045	0.9918	0.0082
17	0.0021	0.9963	0.0037
18	0.0009	0.9984	0.0016
19	0.0004	0.9993	0.0007
20	0.0002	0.9997	0.0003
21	0.0001	0.9999	0.0001
22	0.0000	1.0000	0.0000
23	0.0000	1.0000	0.0000

sequencing redundancy 9-fold (`\rho / h = 9.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0001	0.0000	1.0000
1	0.0011	0.0001	0.9999
2	0.0050	0.0012	0.9988
3	0.0150	0.0062	0.9938
4	0.0337	0.0212	0.9788
5	0.0607	0.0550	0.9450
6	0.0911	0.1157	0.8843
7	0.1171	0.2068	0.7932
8	0.1318	0.3239	0.6761
9	0.1318	0.4557	0.5443
10	0.1186	0.5874	0.4126
11	0.0970	0.7060	0.2940
12	0.0728	0.8030	0.1970
13	0.0504	0.8758	0.1242
14	0.0324	0.9261	0.0739
15	0.0194	0.9585	0.0415
16	0.0109	0.9780	0.0220
17	0.0058	0.9889	0.0111
18	0.0029	0.9947	0.0053
19	0.0014	0.9976	0.0024
20	0.0006	0.9989	0.0011
21	0.0003	0.9996	0.0004
22	0.0001	0.9998	0.0002
23	0.0000	0.9999	0.0001
24	0.0000	1.0000	0.0000

sequencing redundancy 10-fold (`\rho / h = 10.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
0	0.0000	0.0000	1.0000
1	0.0005	0.0000	1.0000
2	0.0023	0.0005	0.9995
3	0.0076	0.0028	0.9972
4	0.0189	0.0103	0.9897
5	0.0378	0.0293	0.9707
6	0.0631	0.0671	0.9329
7	0.0901	0.1301	0.8699
8	0.1126	0.2202	0.7798
9	0.1251	0.3328	0.6672
10	0.1251	0.4579	0.5421
11	0.1137	0.5830	0.4170
12	0.0948	0.6968	0.3032
13	0.0729	0.7916	0.2084
14	0.0521	0.8645	0.1355
15	0.0347	0.9165	0.0835
16	0.0217	0.9513	0.0487
17	0.0128	0.9730	0.0270
18	0.0071	0.9857	0.0143
19	0.0037	0.9928	0.0072
20	0.0019	0.9965	0.0035
21	0.0009	0.9984	0.0016
22	0.0004	0.9993	0.0007
23	0.0002	0.9997	0.0003
24	0.0001	0.9999	0.0001
25	0.0000	1.0000	0.0000
26	0.0000	1.0000	0.0000

sequencing redundancy 20-fold (`\rho / h = 20.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
4	0.0000	0.0000	1.0000
5	0.0001	0.0000	1.0000
6	0.0002	0.0001	0.9999
7	0.0005	0.0003	0.9997
8	0.0013	0.0008	0.9992
9	0.0029	0.0021	0.9979
10	0.0058	0.0050	0.9950
11	0.0106	0.0108	0.9892
12	0.0176	0.0214	0.9786
13	0.0271	0.0390	0.9610
14	0.0387	0.0661	0.9339
15	0.0516	0.1049	0.8951
16	0.0646	0.1565	0.8435
17	0.0760	0.2211	0.7789
18	0.0844	0.2970	0.7030
19	0.0888	0.3814	0.6186
20	0.0888	0.4703	0.5297
21	0.0846	0.5591	0.4409
22	0.0769	0.6437	0.3563
23	0.0669	0.7206	0.2794
24	0.0557	0.7875	0.2125
25	0.0446	0.8432	0.1568
26	0.0343	0.8878	0.1122
27	0.0254	0.9221	0.0779
28	0.0181	0.9475	0.0525
29	0.0125	0.9657	0.0343
30	0.0083	0.9782	0.0218
31	0.0054	0.9865	0.0135
32	0.0034	0.9919	0.0081
33	0.0020	0.9953	0.0047
34	0.0012	0.9973	0.0027
35	0.0007	0.9985	0.0015
36	0.0004	0.9992	0.0008
37	0.0002	0.9996	0.0004
38	0.0001	0.9998	0.0002
39	0.0001	0.9999	0.0001
40	0.0000	0.9999	0.0001
41	0.0000	1.0000	0.0000
42	0.0000	1.0000	0.0000

sequencing redundancy 25-fold (`\rho / h = 25.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
7	0.0000	0.0000	1.0000
8	0.0001	0.0000	1.0000
9	0.0001	0.0001	0.9999
10	0.0004	0.0002	0.9998
11	0.0008	0.0006	0.9994
12	0.0017	0.0014	0.9986
13	0.0033	0.0031	0.9969
14	0.0059	0.0065	0.9935
15	0.0099	0.0124	0.9876
16	0.0155	0.0223	0.9777
17	0.0227	0.0377	0.9623
18	0.0316	0.0605	0.9395
19	0.0415	0.0920	0.9080
20	0.0519	0.1336	0.8664
21	0.0618	0.1855	0.8145
22	0.0702	0.2473	0.7527
23	0.0763	0.3175	0.6825
24	0.0795	0.3939	0.6061
25	0.0795	0.4734	0.5266
26	0.0765	0.5529	0.4471
27	0.0708	0.6294	0.3706
28	0.0632	0.7002	0.2998
29	0.0545	0.7634	0.2366
30	0.0454	0.8179	0.1821
31	0.0366	0.8633	0.1367
32	0.0286	0.8999	0.1001
33	0.0217	0.9285	0.0715
34	0.0159	0.9502	0.0498
35	0.0114	0.9662	0.0338
36	0.0079	0.9775	0.0225
37	0.0053	0.9854	0.0146
38	0.0035	0.9908	0.0092
39	0.0023	0.9943	0.0057
40	0.0014	0.9966	0.0034
41	0.0009	0.9980	0.0020
42	0.0005	0.9988	0.0012
43	0.0003	0.9993	0.0007
44	0.0002	0.9996	0.0004
45	0.0001	0.9998	0.0002
46	0.0001	0.9999	0.0001
47	0.0000	0.9999	0.0001
48	0.0000	1.0000	0.0000
49	0.0000	1.0000	0.0000

sequencing redundancy 50-fold (`\rho / h = 50.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
24	0.0000	0.0000	1.0000
25	0.0000	0.0000	1.0000
26	0.0001	0.0001	0.9999
27	0.0001	0.0001	0.9999
28	0.0002	0.0003	0.9997
29	0.0004	0.0005	0.9995
30	0.0007	0.0009	0.9991
31	0.0011	0.0016	0.9984
32	0.0017	0.0027	0.9973
33	0.0026	0.0044	0.9956
34	0.0038	0.0070	0.9930
35	0.0054	0.0108	0.9892
36	0.0075	0.0162	0.9838
37	0.0102	0.0238	0.9762
38	0.0134	0.0340	0.9660
39	0.0172	0.0474	0.9526
40	0.0215	0.0646	0.9354
41	0.0262	0.0861	0.9139
42	0.0312	0.1123	0.8877
43	0.0363	0.1435	0.8565
44	0.0412	0.1798	0.8202
45	0.0458	0.2210	0.7790
46	0.0498	0.2669	0.7331
47	0.0530	0.3167	0.6833
48	0.0552	0.3697	0.6303
49	0.0563	0.4249	0.5751
50	0.0563	0.4812	0.5188
51	0.0552	0.5375	0.4625
52	0.0531	0.5927	0.4073
53	0.0501	0.6458	0.3542
54	0.0464	0.6959	0.3041
55	0.0422	0.7423	0.2577
56	0.0376	0.7845	0.2155
57	0.0330	0.8221	0.1779
58	0.0285	0.8551	0.1449
59	0.0241	0.8836	0.1164
60	0.0201	0.9077	0.0923
61	0.0165	0.9278	0.0722
62	0.0133	0.9443	0.0557
63	0.0105	0.9576	0.0424
64	0.0082	0.9682	0.0318
65	0.0063	0.9764	0.0236
66	0.0048	0.9827	0.0173
67	0.0036	0.9875	0.0125
68	0.0026	0.9911	0.0089
69	0.0019	0.9938	0.0062
70	0.0014	0.9957	0.0043
71	0.0010	0.9970	0.0030
72	0.0007	0.9980	0.0020
73	0.0005	0.9987	0.0013
74	0.0003	0.9991	0.0009
75	0.0002	0.9994	0.0006
76	0.0001	0.9996	0.0004
77	0.0001	0.9998	0.0002
78	0.0001	0.9999	0.0001
79	0.0000	0.9999	0.0001
80	0.0000	0.9999	0.0001
81	0.0000	1.0000	0.0000
82	0.0000	1.0000	0.0000
83	0.0000	1.0000	0.0000

sequencing redundancy 75-fold (`\rho / h = 75.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
42	0.0000	0.0000	1.0000
43	0.0000	0.0000	1.0000
44	0.0000	0.0000	1.0000
45	0.0001	0.0001	0.9999
46	0.0001	0.0001	0.9999
47	0.0001	0.0002	0.9998
48	0.0002	0.0004	0.9996
49	0.0003	0.0006	0.9994
50	0.0005	0.0009	0.9991
51	0.0007	0.0014	0.9986
52	0.0011	0.0021	0.9979
53	0.0015	0.0032	0.9968
54	0.0021	0.0047	0.9953
55	0.0028	0.0068	0.9932
56	0.0038	0.0096	0.9904
57	0.0050	0.0134	0.9866
58	0.0065	0.0184	0.9816
59	0.0082	0.0249	0.9751
60	0.0103	0.0331	0.9669
61	0.0126	0.0433	0.9567
62	0.0153	0.0560	0.9440
63	0.0182	0.0712	0.9288
64	0.0213	0.0894	0.9106
65	0.0246	0.1107	0.8893
66	0.0279	0.1353	0.8647
67	0.0313	0.1632	0.8368
68	0.0345	0.1945	0.8055
69	0.0375	0.2290	0.7710
70	0.0402	0.2665	0.7335
71	0.0424	0.3066	0.6934
72	0.0442	0.3490	0.6510
73	0.0454	0.3932	0.6068
74	0.0460	0.4386	0.5614
75	0.0460	0.4846	0.5154
76	0.0454	0.5307	0.4693
77	0.0442	0.5761	0.4239
78	0.0425	0.6203	0.3797
79	0.0404	0.6628	0.3372
80	0.0379	0.7032	0.2968
81	0.0350	0.7411	0.2589
82	0.0321	0.7761	0.2239
83	0.0290	0.8082	0.1918
84	0.0259	0.8371	0.1629
85	0.0228	0.8630	0.1370
86	0.0199	0.8858	0.1142
87	0.0172	0.9057	0.0943
88	0.0146	0.9229	0.0771
89	0.0123	0.9375	0.0625
90	0.0103	0.9498	0.0502
91	0.0085	0.9601	0.0399
92	0.0069	0.9685	0.0315
93	0.0056	0.9754	0.0246
94	0.0044	0.9810	0.0190
95	0.0035	0.9854	0.0146
96	0.0027	0.9889	0.0111
97	0.0021	0.9917	0.0083
98	0.0016	0.9938	0.0062
99	0.0012	0.9954	0.0046
100	0.0009	0.9966	0.0034
101	0.0007	0.9976	0.0024
102	0.0005	0.9983	0.0017
103	0.0004	0.9988	0.0012
104	0.0003	0.9991	0.0009
105	0.0002	0.9994	0.0006
106	0.0001	0.9996	0.0004
107	0.0001	0.9997	0.0003
108	0.0001	0.9998	0.0002
109	0.0000	0.9999	0.0001
110	0.0000	0.9999	0.0001
111	0.0000	0.9999	0.0001
112	0.0000	1.0000	0.0000
113	0.0000	1.0000	0.0000
114	0.0000	1.0000	0.0000
115	0.0000	1.0000	0.0000

sequencing redundancy 100-fold (`\rho / h = 100.0`)

`\phi`	`P_{h,\phi} - P_{h,\phi+1}`	`1-P_{h,\phi}`	`P_{h,\phi}`
61	0.0000	0.0000	1.0000
62	0.0000	0.0000	1.0000
63	0.0000	0.0000	1.0000
64	0.0000	0.0000	1.0000
65	0.0000	0.0001	0.9999
66	0.0001	0.0001	0.9999
67	0.0001	0.0002	0.9998
68	0.0002	0.0003	0.9997
69	0.0002	0.0004	0.9996
70	0.0003	0.0007	0.9993
71	0.0004	0.0010	0.9990
72	0.0006	0.0014	0.9986
73	0.0008	0.0020	0.9980
74	0.0011	0.0028	0.9972
75	0.0015	0.0040	0.9960
76	0.0020	0.0055	0.9945
77	0.0026	0.0074	0.9926
78	0.0033	0.0100	0.9900
79	0.0042	0.0133	0.9867
80	0.0052	0.0175	0.9825
81	0.0064	0.0226	0.9774
82	0.0078	0.0291	0.9709
83	0.0094	0.0369	0.9631
84	0.0112	0.0463	0.9537
85	0.0132	0.0575	0.9425
86	0.0154	0.0708	0.9292
87	0.0176	0.0861	0.9139
88	0.0201	0.1038	0.8962
89	0.0225	0.1238	0.8762
90	0.0250	0.1463	0.8537
91	0.0275	0.1714	0.8286
92	0.0299	0.1989	0.8011
93	0.0322	0.2288	0.7712
94	0.0342	0.2610	0.7390
95	0.0360	0.2952	0.7048
96	0.0375	0.3312	0.6688
97	0.0387	0.3687	0.6313
98	0.0395	0.4074	0.5926
99	0.0399	0.4468	0.5532
100	0.0399	0.4867	0.5133
101	0.0395	0.5266	0.4734
102	0.0387	0.5660	0.4340
103	0.0376	0.6047	0.3953
104	0.0361	0.6423	0.3577
105	0.0344	0.6784	0.3216
106	0.0325	0.7128	0.2872
107	0.0303	0.7453	0.2547
108	0.0281	0.7756	0.2244
109	0.0258	0.8037	0.1963
110	0.0234	0.8294	0.1706
111	0.0211	0.8529	0.1471
112	0.0188	0.8740	0.1260
113	0.0167	0.8928	0.1072
114	0.0146	0.9095	0.0905
115	0.0127	0.9241	0.0759
116	0.0110	0.9368	0.0632
117	0.0094	0.9478	0.0522
118	0.0079	0.9572	0.0428
119	0.0067	0.9651	0.0349
120	0.0056	0.9718	0.0282
121	0.0046	0.9773	0.0227
122	0.0038	0.9819	0.0181
123	0.0031	0.9857	0.0143
124	0.0025	0.9888	0.0112
125	0.0020	0.9912	0.0088
126	0.0016	0.9932	0.0068
127	0.0012	0.9948	0.0052
128	0.0010	0.9960	0.0040
129	0.0007	0.9970	0.0030
130	0.0006	0.9977	0.0023
131	0.0004	0.9983	0.0017
132	0.0003	0.9987	0.0013
133	0.0003	0.9991	0.0009
134	0.0002	0.9993	0.0007
135	0.0001	0.9995	0.0005
136	0.0001	0.9996	0.0004
137	0.0001	0.9997	0.0003
138	0.0001	0.9998	0.0002
139	0.0000	0.9999	0.0001
140	0.0000	0.9999	0.0001
141	0.0000	0.9999	0.0001
142	0.0000	1.0000	0.0000
143	0.0000	1.0000	0.0000
144	0.0000	1.0000	0.0000
145	0.0000	1.0000	0.0000

VIEW ALL

news + thoughts

Propensity score weighting

Mon 17-03-2025

The needs of the many outweigh the needs of the few. —Mr. Spock (Star Trek II)

This month, we explore a related and powerful technique to address bias: propensity score weighting (PSW), which applies weights to each subject instead of matching (or discarding) them.

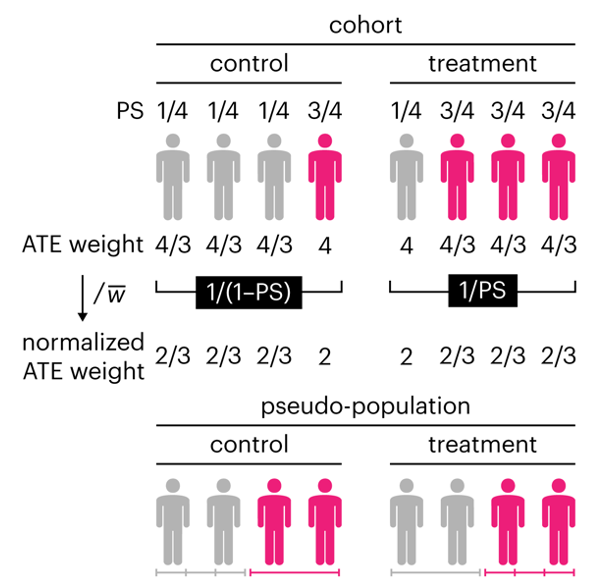
Martin Krzywinski @MKrzywinski mkweb.bcgsc.ca

▲ Nature Methods Points of Significance column: Propensity score weighting. (read)

Kurz, C.F., Krzywinski, M. & Altman, N. (2025) Points of significance: Propensity score weighting. Nat. Methods 22:1–3.

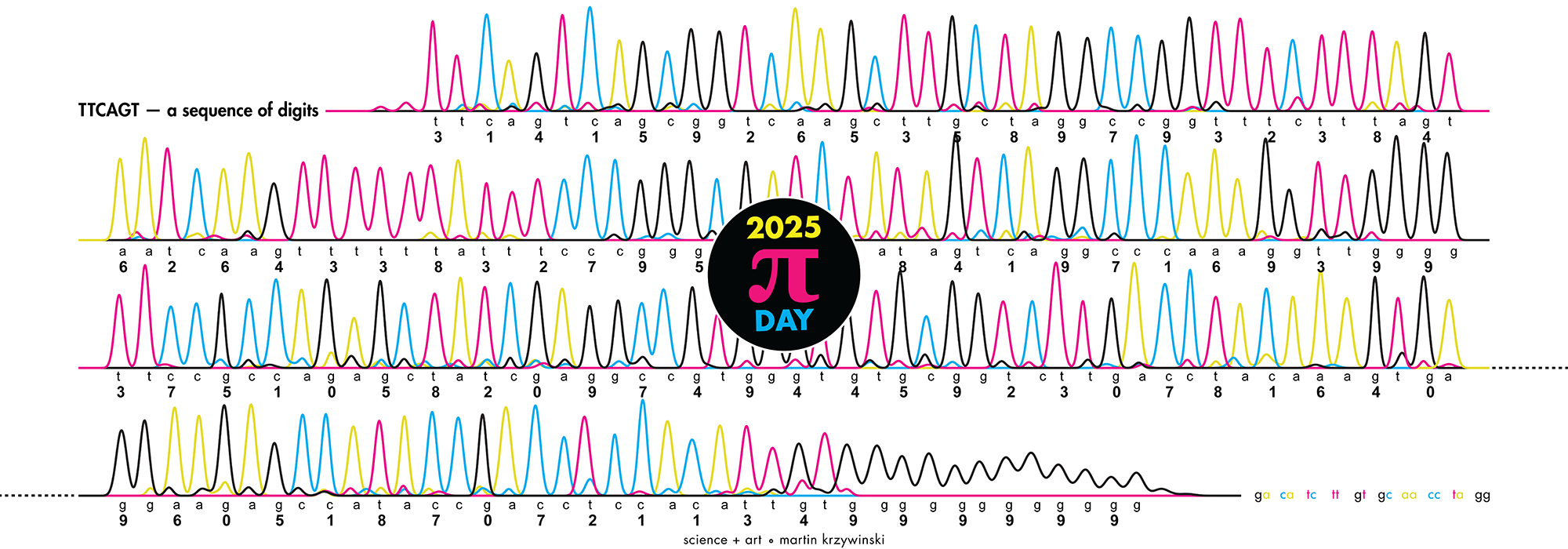
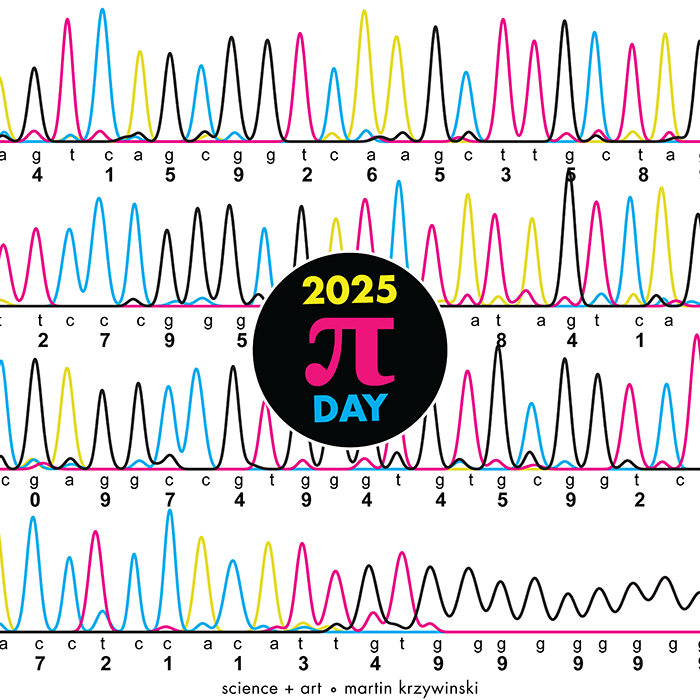
Happy 2025 π Day—
TTCAGT: a sequence of digits

Thu 13-03-2025

Celebrate π Day (March 14th) and sequence digits like its 1999. Let's call some peaks.

▲ 2025 π DAY | TTCAGT: a sequence of digits. The digits of π are encoded into DNA sequence and visualized with Sanger sequencing. (details)

Crafting 10 Years of Statistics Explanations: Points of Significance

Sun 09-03-2025

I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player

Points of Significance is an ongoing series of short articles about statistics in Nature Methods that started in 2013. Its aim is to provide clear explanations of essential concepts in statistics for a nonspecialist audience. The articles favor heuristic explanations and make extensive use of simulated examples and graphical explanations, while maintaining mathematical rigor.

Topics range from basic, but often misunderstood, such as uncertainty and P-values, to relatively advanced, but often neglected, such as the error-in-variables problem and the curse of dimensionality. More recent articles have focused on timely topics such as modeling of epidemics, machine learning, and neural networks.

In this article, we discuss the evolution of topics and details behind some of the story arcs, our approach to crafting statistical explanations and narratives, and our use of figures and numerical simulations as props for building understanding.

▲ Crafting 10 Years of Statistics Explanations: Points of Significance. (read)

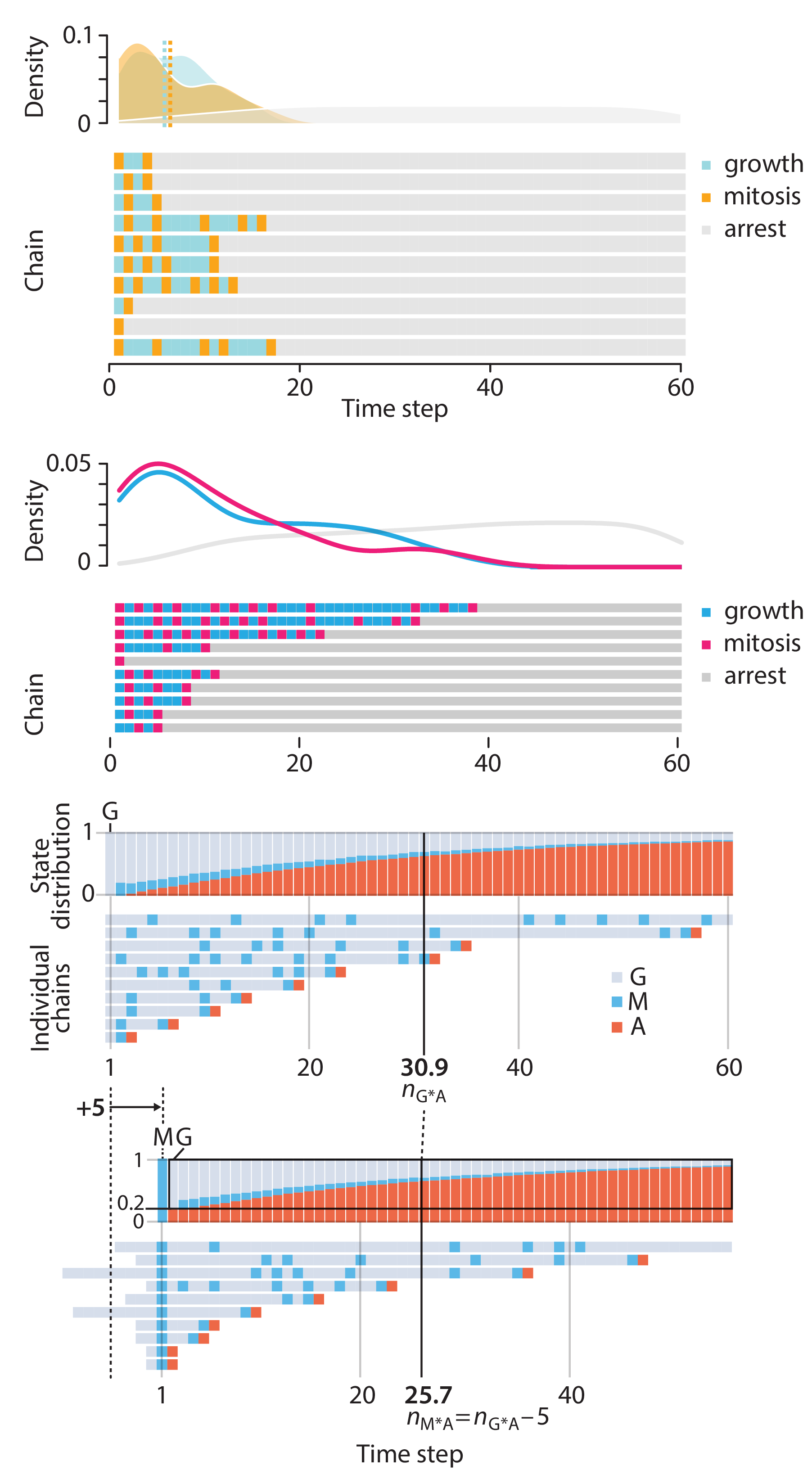
Altman, N. & Krzywinski, M. (2025) Crafting 10 Years of Statistics Explanations: Points of Significance. Annual Review of Statistics and Its Application 12:69–87.

Propensity score matching

Mon 16-09-2024

I don’t have good luck in the match points. —Rafael Nadal, Spanish tennis player

In many experimental designs, we need to keep in mind the possibility of confounding variables, which may give rise to bias in the estimate of the treatment effect.

▲ Nature Methods Points of Significance column: Propensity score matching. (read)

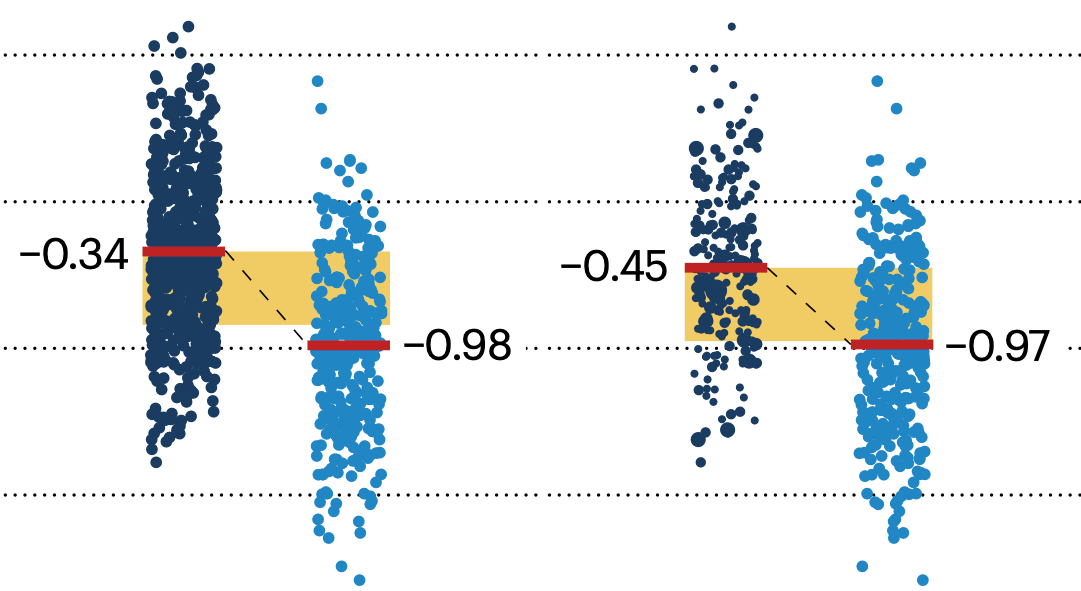
If the control and experimental groups aren't matched (or, roughly, similar enough), this bias can arise.

Sometimes this can be dealt with by randomizing, which on average can balance this effect out. When randomization is not possible, propensity score matching is an excellent strategy to match control and experimental groups.

Kurz, C.F., Krzywinski, M. & Altman, N. (2024) Points of significance: Propensity score matching. Nat. Methods 21:1770–1772.

Understanding p-values and significance

Tue 24-09-2024

P-values combined with estimates of effect size are used to assess the importance of experimental results. However, their interpretation can be invalidated by selection bias when testing multiple hypotheses, fitting multiple models or even informally selecting results that seem interesting after observing the data.

We offer an introduction to principled uses of p-values (targeted at the non-specialist) and identify questionable practices to be avoided.

▲ Understanding p-values and significance. (read)

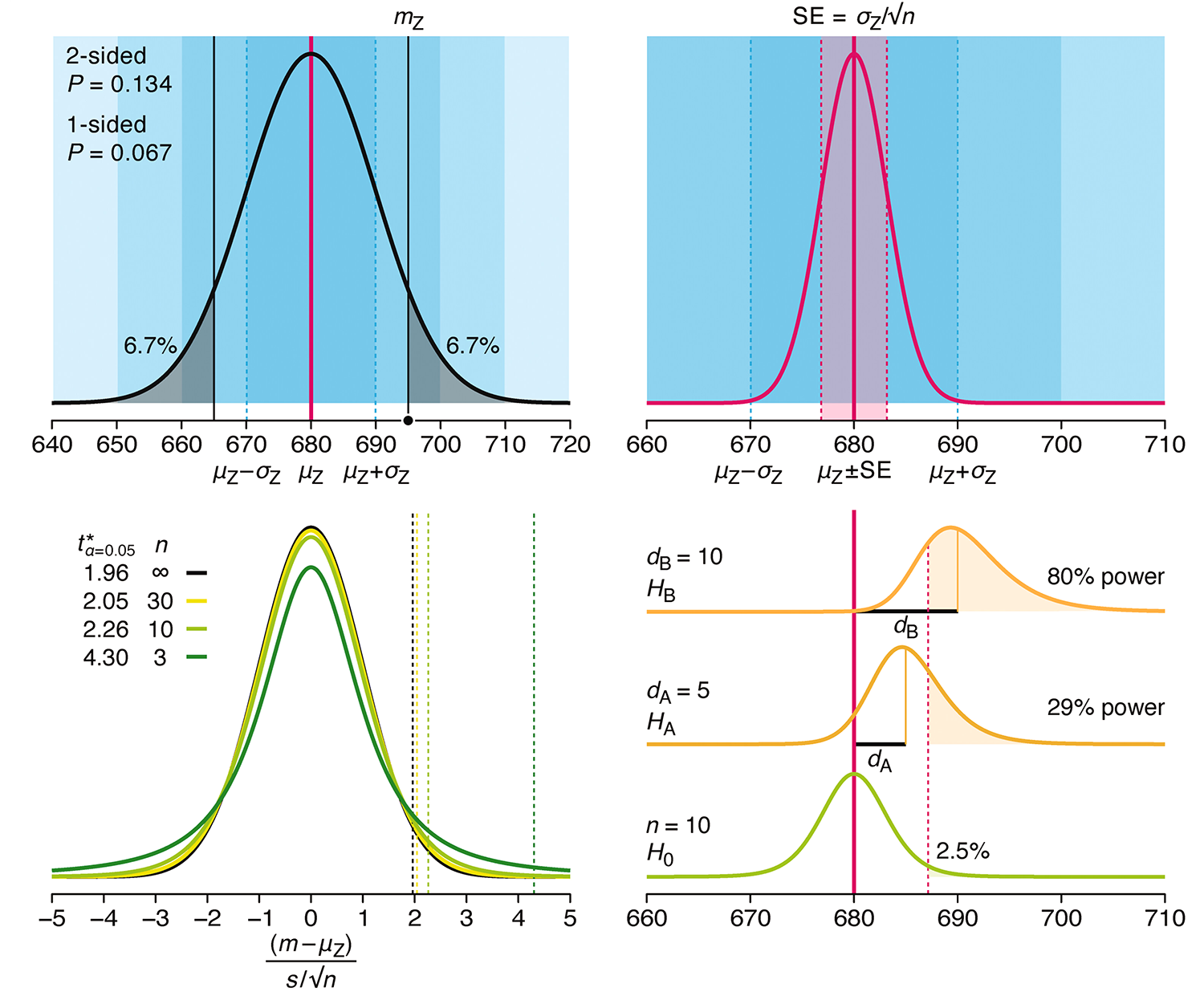
Altman, N. & Krzywinski, M. (2024) Understanding p-values and significance. Laboratory Animals 58:443–446.

Depicting variability and uncertainty using intervals and error bars

Thu 05-09-2024

Variability is inherent in most biological systems due to differences among members of the population. Two types of variation are commonly observed in studies: differences among samples and the “error” in estimating a population parameter (e.g. mean) from a sample. While these concepts are fundamentally very different, the associated variation is often expressed using similar notation—an interval that represents a range of values with a lower and upper bound.

In this article we discuss how common intervals are used (and misused).

▲ Depicting variability and uncertainty using intervals and error bars. (read)

Altman, N. & Krzywinski, M. (2024) Depicting variability and uncertainty using intervals and error bars. Laboratory Animals 58:453–456.